Van der Pauw 法とは、薄膜と呼ばれるような薄いシート状物質の電気抵抗率 \(\rho\) や電気伝導率 \(\sigma\) を求めるために用いられている測定手法である。Van der Pauw 法の優れている点は、試料の2次元的な形状によらず、どのような形の試料に対してもその測定法を適用できるところにある。以下では Van der Pauw 法の原理を解説する。
Van der Pauw 法の概要
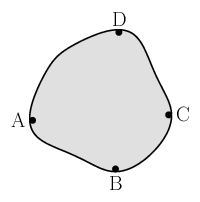
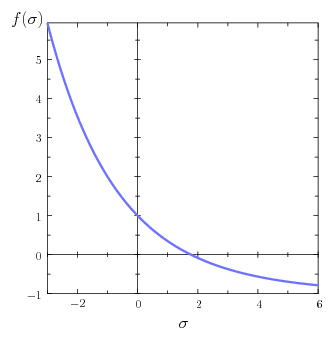
物質全体で一様な電気抵抗率 \(\rho\) をもったシート状物質を考えよう。シートの厚さ \(d\) は場所によらず一定であるとするが、その平面的な形状は、途中に穴さえ存在していなければどのような形であってもよい。また、この物質の外周にはその電気抵抗率を測定するために4つの小さな金属電極 \(\mr{A},\mr{B},\mr{C},\mr{D}\) が取り付けられている。このとき、このシート状物質の電気伝導率(導電率)\(\sigma=1/\rho\) は、次の方程式を解くことで知ることができる: \begin{equation} \exp( -\pi d R_{\mr{A}} \1 \sigma ) + \exp( -\pi d R_{\mr{B}} \2 \sigma ) = 1 \label{pauw} \end{equation} ただし、抵抗と同じ次元をもった2つの量 \(R_{\mr{A}},R_{\mr{B}}\) は次の式によって定義される: \begin{equation} R_{\mr{A}} = \frac{V_{\mr{D}}-V_{\mr{C}}}{I_{\mr{AB}}}, \5 R_{\mr{B}} = \frac{V_{\mr{A}}-V_{\mr{D}}}{I_{\mr{BC}}} \label{r} \end{equation} ここで \(I_{XY}\) とは、異なる2つの金属電極 \(X\) と \(Y\) に直流電源をつないだときに、物質を通って電極 \(X\) から電極 \(Y\) のほうへ流れていった電流の大きさを表す。また \(V_{Z}\) とは、そのような電流が流れている状況における電極 \(Z\) の電位である。直流電源や電流計、電圧計を用意すれば \(I_{XY}\) や \(V_{Z}\) は簡単に測定することができるから、あとはシートの厚さを測定して方程式\eqref{pauw}を解くだけで、試料の形状によらず導電率 \(\sigma\) を決定することができる。式\eqref{pauw}は超越方程式であり、これを \(\sigma\) について代数的に解くことはできないのだが、コンピューターを用いれば解は簡単に求まる。とくにこの問題ではニュートン法が便利で \begin{equation} f(\sigma) = \exp( -\pi d R_{\mr{A}} \1 \sigma ) + \exp( -\pi d R_{\mr{B}} \2 \sigma ) - 1 \end{equation} という関数にニュートン法を適用すれば、\(\sigma\) の初期値の与え方によらず \(f(\sigma)=0\) の唯一の解へ必ず収束してくれる。
先にも述べたが、van der Pauw 法を用いるためには試料のある平面内に穴が存在してはならない(例えば、中身の詰まった円盤形の試料はよいが、その中心に穴の空いたドーナツ形はダメである)。一般に van der Pauw 法を適用するにあたっては次のような点に注意する必要がある:
- 4つの電極は試料の外周上に取り付けられている。
- 電極の大きさは十分に小さい。
- 試料は厚さ方向に一様である。
- 試料の表面は単連結である。すなわち穴が存在しない。
なぜこれらの条件が必要になるのか、また、シート状物質の形状によらず方程式\eqref{pauw}を解くことで導電率を求められるのはなぜか、以下では van der Pauw 法の数学的背景について詳しく見ていくことにしよう(数学的詳細に興味がない場合、この先は読まなくてもよい)。
半無限シート状物質の場合
Van der Pauw 法は穴の存在しない任意形状のシート状物質に対して適用可能な測定手法であるが、まずはその特別な場合として上半平面全体に半無限的に広がったシート状試料で式\eqref{pauw}が成り立つことを示そう。
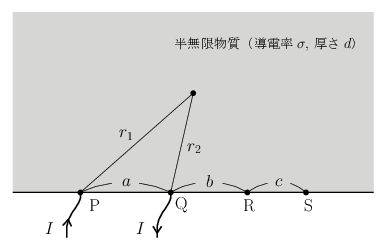
上の図に示したように、上半平面全体に広がるシート状物質の境界上には4つの小さな金属電極 \(\mr{P},\mr{Q},\mr{R},\mr{S}\) が取り付けられており、電極 \(\mr{P}\) から電極 \(\mr{Q}\) のほうへ、物質を通して一定の電流 \(I\) が流されている。このとき物質上の任意の点における電位(スカラーポテンシャル)\(\phi\) は次の式で与えられる: \begin{equation} \phi = \frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{r_{2}}{r_{1}} \Bigr) \label{phi} \end{equation} ただし \(r_{1},r_{2}\) はそれぞれ電極 \(\mr{P},\mr{Q}\) から測った電位の測定点までの距離を表す(この式の導出は1つ前の記事「定常電流」で行っているので、ここでは省略する)。なお、この式では電位の基準点を無限遠点としている(無限遠点で \(\phi=0\) となる)。さて、今、境界上に取り付けられた4つの電極間の距離を上の図のように \(a,b,c\) と置くことにしよう。このとき電極 \(\mr{R}\) の電位 \(\phi_{\mr{R}}^{\,}\) は、式\eqref{phi}から簡単に計算することができて \begin{equation} \phi_{\mr{R}}^{\,} = \frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{b}{a+b} \Bigr) \end{equation} となる。同様にして電極 \(\mr{S}\) の電位 \(\phi_{\mr{S}}^{\,}\) を計算すると \begin{equation} \phi_{\mr{S}}^{\,} = \frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{b+c}{a+b+c} \Bigr) \end{equation} となるので、電極 \(\mr{R}\) と電極 \(\mr{S}\) の電位差(電圧)は \begin{equation} \phi_{\mr{S}}^{\,} - \phi_{\mr{R}}^{\,} = \frac{I}{\pi d\sigma} \, \ln \biggl( \frac{(a+b)(b+c)}{b(a+b+c)} \biggr) \label{phisr} \end{equation} で与えられることがわかる。
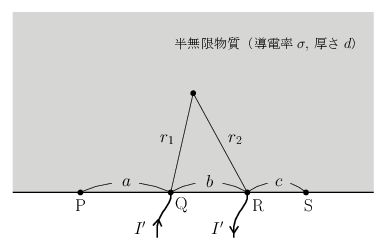
次に電流の流し方を少し変えて、電極 \(\mr{Q}\) から電極 \(\mr{R}\) のほうへ一定の電流 \(I'\) が流れるようにしてみよう。上の図のように電極 \(\mr{Q},\mr{R}\) から測った長さをそれぞれ \(r_{1},r_{2}\) と置くことにすると、物質上の任意の点における電位 \(\phi\) は先ほどと同じように \begin{equation} \phi = \frac{I'}{\pi d\sigma} \, \ln \Bigl( \frac{r_{2}}{r_{1}} \Bigr) \end{equation} から計算することができるので、電極 \(\mr{S}\) の電位 \(\phi_{\mr{S}}^{\,}\) は \begin{equation} \phi_{\mr{S}}^{\,} = \frac{I'}{\pi d\sigma} \, \ln \Bigl( \frac{c}{b+c} \Bigr) \end{equation} となり、電極 \(\mr{P}\) の電位 \(\phi_{\mr{P}}^{\,}\) は \begin{equation} \phi_{\mr{P}}^{\,} = \frac{I'}{\pi d\sigma} \, \ln \Bigl( \frac{a+b}{a} \Bigr) \end{equation} となる。これより電極 \(\mr{S}\) と電極 \(\mr{P}\) の電位差は \begin{equation} \phi_{\mr{P}}^{\,} - \phi_{\mr{S}}^{\,} = \frac{I'}{\pi d\sigma} \, \ln \biggl( \frac{(a+b)(b+c)}{ac} \biggr) \label{phips} \end{equation} になる。
以上、異なる2つの実験的配置で電位差を計算することができたが、ここで式\eqref{phisr}と\eqref{phips}を参考にして次のような量を定義する: \begin{align} R_{\mr{P}} &= \frac{\phi_{\mr{S}}^{\,}-\phi_{\mr{R}}^{\,}}{I_{\mr{PQ}}} = \frac{1}{\pi d\sigma} \, \ln \biggl( \frac{(a+b)(b+c)}{b(a+b+c)} \biggr) \\[10pt] R_{\mr{Q}} &= \frac{\phi_{\mr{P}}^{\,}-\phi_{\mr{S}}^{\,}}{I_{\mr{QR}}} = \frac{1}{\pi d\sigma} \, \ln \biggl( \frac{(a+b)(b+c)}{ac} \biggr) \end{align} ただし、どの電極からどの電極へ電流を流したのかが分かりやすくなるように \(I,I'\) をそれぞれ \(I_{\mr{PQ}},I_{\mr{QR}}\) と書き直した。\(R_{\mr{P}}\) や \(R_{\mr{Q}}\) は抵抗と同じ次元をもっており、これらが電流の大きさに依存しない量となっていることに注意しよう。これらを用いて次のような計算を行ってみる: \begin{equation} \exp( -\pi d R_{\mr{P}} \2 \sigma ) + \exp( -\pi d R_{\mr{Q}} \2 \sigma ) = \frac{b(a+b+c)}{(a+b)(b+c)} + \frac{ac}{(a+b)(b+c)} = 1 \end{equation} この結果は半無限物質の場合における式\eqref{pauw}になっている。したがって、少なくとも上半平面全体に広がったシート状物質に対しては、関係式 \begin{equation} \exp( -\pi d R_{\mr{P}} \2 \sigma ) + \exp( -\pi d R_{\mr{Q}} \2 \sigma ) = 1 \end{equation} の成り立っていることがわかった。
一般的な形状の物質
任意の形のシート状物質で式\eqref{pauw}が成り立つことを証明するにはどのようにすればよいだろう? それには半無限物質の場合と同じようにして、ラプラス方程式 \begin{equation} \nabla^{2} V = 0 \end{equation} を境界条件 \begin{align} \nabla &V \cdot \bm{n} = 0 & &\text{(物質とまわりの空間の境界面上において)} \\[5pt] &V = \text{一定} & &\text{(物質と電極 \(Z\) の境界面 \(S_{Z}\) 上において)} \\[3pt] \int_{S_{Z}} \nabla V &\cdot \bm{n} \, dS = \frac{I_{Z}}{\sigma} & &\text{(\(\,Z=\mr{A},\mr{B},\mr{C},\mr{D}\,\))} \end{align} の下で解き、得られたスカラーポテンシャルから計算した抵抗 \(R_{\mr{A}}\) や \(R_{\mr{B}}\) が van der Pauw の関係式\eqref{pauw}を満足することを言えばよい(ラプラス方程式や境界条件についての詳細は1つ前の記事「定常電流」を参照)。しかしながら、一般的な状況においてラプラス方程式を解析的に解くことは非常に難しく、とくにシート状物質の形状が明確に与えられていない今の問題では不可能と言ってよい。そこで別の手段を使ってラプラス方程式の解を構成する。実は、複素関数の性質を使うことでラプラス方程式を具体的に解かなくともその解を見つけることができてしまう。
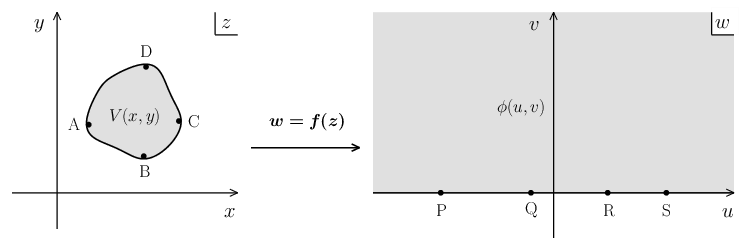
上の図に示したように、任意形状のシート状物質表面に広がった複素 \(z\) 平面を考えよう(ただし物質に穴は空いていないものとする)。また、それとは別にもう1つ、図の右側に示したような複素 \(w\) 平面も用意しておく。ここで次の定理を利用する。
単純閉曲線とは自分自身とは交わらない閉じた曲線のことである。この定理は、複素関数論における「カラテオドリの定理」の系なのだが、カラテオドリの定理の証明が難しいため、上で述べた定理の証明も省略する。ここではひとまず、任意の形状のシート状物質に対して、上の図に示したような正則関数 \(w=f(z)\) が存在することを認めればよい(\(\,f(z)\) が具体的にどのような関数になるかは知らなくてよい)。ちなみに「1対1に連続に写像される」というのは、近い点は近い点へ、遠い点は遠い点へ、また異なる2つの点は異なる2つの点へ写されるという意味である。例えば上の図で、2つの点 \(\mr{A},\mr{B}\) が関数 \(f\) によって \(\mr{A}\to\mr{P},\ \mr{B}\to\mr{Q}\) と写されたのなら、残りの2つの点は \(\mr{C}\to\mr{R},\ \mr{D}\to\mr{S}\) のように写されるわけで、\(\mr{C}\to\mr{S},\ \mr{D}\to\mr{R}\) という順番で写ることはない。
さて、正則関数 \(w=f(z)\) を実部と虚部に分けて書いて \begin{equation} w = f(z) = u(x,y) + i v(x,y) \end{equation} と表してみよう(\(\,u(x,y),v(x,y)\) は実関数)。ただし、\(z=x+iy\) である。また \(w=u+iv\) とするとき、\(uv\)-平面上の上半平面に置かれた半無限物質のスカラーポテンシャル \(\phi=\phi(u,v)\) は解析的に求めることができて、それは \begin{equation} \phi(u,v) = \frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{r_{2}}{r_{1}} \Bigr) \label{phiuv} \end{equation} という形になる(陽には書いていないが、電流の出入りする電極から上半平面のある点までの距離 \(r_{1},r_{2}\) は直交座標 \((u,v)\) を用いて表せる)。電極から物質に流す電流の大きさが \(xy\)-平面と \(uv\)-平面に共通であるとすれば、実は \begin{equation} V(x,y) = \phi( u(x,y), v(x,y) ) \label{v} \end{equation} という関数が \(xy\)-平面上における電位を表す関数となる。これがなぜ正しいのかという確認は次節で行うことにして、ひとまずはこの事実を認めることにすれば次の関係式 \begin{equation} \exp( -\pi d R_{\mr{A}} \1 \sigma ) + \exp( -\pi d R_{\mr{B}} \2 \sigma ) = 1 \label{pauw2} \end{equation} \begin{equation} R_{\mr{A}} = \frac{V_{\mr{D}}-V_{\mr{C}}}{I_{\mr{AB}}}, \5 R_{\mr{B}} = \frac{V_{\mr{A}}-V_{\mr{D}}}{I_{\mr{BC}}} \label{r2} \end{equation} が成り立つことは簡単にわかる。今 \(xy\)-平面から \(uv\)-平面への写像 \(u=u(x,y),\,v=v(x,y)\) によって、物質に取り付けられた4つの電極 \(\mr{A},\mr{B},\mr{C},\mr{D}\) が \(uv\)-平面の実軸上(または無限遠点)にある \(\mr{P},\mr{Q},\mr{R},\mr{S}\) へこの順番で写ったとしよう(このときの電極間距離は具体的に分からなくてもよい)。このとき式\eqref{v}から \begin{equation} V_{\mr{A}} = \phi_{\mr{P}}^{\,}, \3 V_{\mr{B}} = \phi_{\mr{Q}}^{\,}, \3 V_{\mr{C}} = \phi_{\mr{R}}^{\,}, \3 V_{\mr{D}} = \phi_{\mr{S}}^{\,} \end{equation} が言える。ところが半無限シート状物質においては \begin{equation} \exp( -\pi d R_{\mr{P}} \2 \sigma ) + \exp( -\pi d R_{\mr{Q}} \2 \sigma ) = 1 \label{pauw3} \end{equation} \begin{equation} R_{\mr{P}} = \frac{\phi_{\mr{S}}^{\,}-\phi_{\mr{R}}^{\,}}{I_{\mr{PQ}}}, \5 R_{\mr{Q}} = \frac{\phi_{\mr{P}}^{\,}-\phi_{\mr{S}}^{\,}}{I_{\mr{QR}}} \label{r3} \end{equation} という関係が成り立っているのであるから、式\eqref{v}の前で仮定している \(I_{\mr{AB}}=I_{\mr{PQ}},\ I_{\mr{BC}}=I_{\mr{QR}}\) という状況では、式\eqref{pauw2}-\eqref{r2}は式\eqref{pauw3}-\eqref{r3}とまったく同一のものになる。よって、任意の形状のシート状物質において van der Pauw の関係式\eqref{pauw2}が成り立つことがわかった。ここで重要なことは、van der Pauw の関係式に半無限物質における電極間距離(前節では \(a,b,c\) と書いた)が含まれていないことにある。\(uv\)-平面における電極間距離は元の物質の形状に応じて様々に変わるものであるはずで、式\eqref{v}が正しいとわかっていても、結局のところ \(f(z)\) の具体形がわからないままでは \(V(x,y)\) の値を計算することなどできないのだが、式\eqref{pauw3}からは \(a,b,c\) という電極間距離に関する情報がうまくキャンセルしてくれているので、\(V(x,y)\) の具体形を気にすることなく、どのような形状の物質に対しても van der Pauw の関係式は実用的に利用できるのである。
ポテンシャル \(\bm{V(x,y)}\) がラプラス方程式の解であることの証明
それでは最後に \begin{equation} V(x,y) = \phi( u(x,y), v(x,y) ) \label{v2} \end{equation} が正しく任意形状のシート状物質の電位を表すことを証明しよう。これを示すには、半無限物質における電位 \(\phi\) が \(uv\)-平面におけるラプラス方程式 \begin{equation} \nabla^{2} \phi = 0 \label{laplace} \end{equation} と境界条件 \begin{align} \nabla &\phi \cdot \bm{n} = 0 & &\text{(物質とまわりの空間の境界面上において)} \label{boundary1} \\[5pt] &\phi = \text{一定} & &\text{(物質と電極 \(W\) の境界面 \(S_{W}\) 上において)} \label{boundary2} \\[3pt] \int_{S_{W}^{\,}} \nabla \phi &\cdot \bm{n} \, dS = \frac{I_{W}}{\sigma} & &\text{(\(\,W=\mr{P},\mr{Q},\mr{R},\mr{S}\,\))} \label{boundary3} \end{align} を満足しているときに、式\eqref{v2}によって構成した \(V\) が \(xy\)-平面におけるラプラス方程式 \begin{equation} \nabla^{2} V = 0 \label{laplace2} \end{equation} と境界条件 \begin{align} \nabla &V \cdot \bm{n} = 0 & &\text{(物質とまわりの空間の境界面上において)} \label{boundary4} \\[5pt] &V = \text{一定} & &\text{(物質と電極 \(Z\) の境界面 \(S_{Z}\) 上において)} \label{boundary5} \\[3pt] \int_{S_{Z}^{\,}} \nabla V &\cdot \bm{n} \, dS = \frac{I_{Z}}{\sigma} & &\text{(\(\,Z=\mr{A},\mr{B},\mr{C},\mr{D}\,\))} \label{boundary6} \end{align} を満足することを言えばよい。ただし、\(w=f(z)\) によって対応する電極どうしには同じ大きさの電流を流すものとする: \begin{equation} I_{Z} = I_{W} \4 \text{(\(\,w=f(z)\) により対応する電極同士)} \end{equation}
まず、式\eqref{laplace}が成り立つならば式\eqref{laplace2}が成り立つこと、すなわち \begin{equation} \biggl( \frac{\d^{2}}{\d u^{2}} + \frac{\d^{2}}{\d v^{2}} \biggr) \phi(u,v) = 0 \end{equation} であるときに \begin{equation} \biggl( \frac{\d^{2}}{\d x^{2}} + \frac{\d^{2}}{\d y^{2}} \biggr) V(x,y) = 0 \label{laplace3} \end{equation} となることを示そう。(より正確には、厚さ方向(\(\,t\) と表そう)の微分演算子も必要で、ラプラシアンは \begin{equation} \frac{\d^{2}}{\d u^{2}} + \frac{\d^{2}}{\d v^{2}} + \frac{\d^{2}}{\d t^{2}}, \5 \frac{\d^{2}}{\d x^{2}} + \frac{\d^{2}}{\d y^{2}} + \frac{\d^{2}}{\d t^{2}} \end{equation} などと書くべきところであるが、今は電位 \(\phi\) や \(V\) が厚さ方向に変化しないことを仮定しているので \(t\) の微分は省略する。) 実は、電位 \(\phi\) だけでなく正則関数 \begin{equation} f(z) = u(x,y) + i v(x,y) \end{equation} の実部や虚部もラプラス方程式を満足する: \begin{equation} \biggl( \frac{\d^{2}}{\d x^{2}} + \frac{\d^{2}}{\d y^{2}} \biggr) u(x,y) = 0, \4 \biggl( \frac{\d^{2}}{\d x^{2}} + \frac{\d^{2}}{\d y^{2}} \biggr) v(x,y) = 0 \end{equation} これは \(f(z)\) が正則関数であるために、その実部 \(u(x,y)\) や虚部 \(v(x,y)\) がコーシー・リーマンの微分方程式 \begin{equation} \frac{\d u}{\d x} = \frac{\d v}{\d y}, \4 \frac{\d u}{\d y} = -\frac{\d v}{\d x} \label{cauchy} \end{equation} を満足することから簡単に示せる: \begin{align*} &\frac{\d^{2} u}{\d x^{2}} = \frac{\d}{\d x} \biggl( \frac{\d v}{\d y} \biggr) = \frac{\d}{\d y} \biggl( \frac{\d v}{\d x} \biggr) = -\frac{\d^{2} u}{\d y^{2}} \\[8pt] &\frac{\d^{2} v}{\d x^{2}} = -\frac{\d}{\d x} \biggl( \frac{\d u}{\d y} \biggr) = -\frac{\d}{\d y} \biggl( \frac{\d u}{\d x} \biggr) = -\frac{\d^{2} v}{\d y^{2}} \end{align*} (正則関数は無限回微分可能なので偏微分の順序を自由に変えてよい。) 逆に、ラプラス方程式を満足するようなある実関数が与えられたときに、それを実部とするような正則関数を作ることが可能である。この事実を用いると、半無限物質の電位 \(\phi(u,v)\) は複素関数に拡張することができて、例えば \begin{equation} \psi(w) = \phi(u,v) + i \chi(u,v) \end{equation} のような正則関数を作ることができる。\(\psi(w)\) は正則関数なので、その実部と虚部はやはりコーシー・リーマンの微分方程式を満足している: \begin{equation} \frac{\d\phi}{\d u} = \frac{\d\chi}{\d v}, \4 \frac{\d\phi}{\d v} = -\frac{\d\chi}{\d u} \label{cauchy2} \end{equation} (実関数 \(\phi\) が与えられたとき、それに共役な実関数 \(\chi\) は任意定数の不定性を除いて一意に定まる。付録でそのような実関数 \(\chi\) を具体的に構成してみよう。) 上の式では \(\psi\) を \(w\) 平面上の正則関数と考えているが \begin{equation} w = f(z) = u(x,y) + i v(x,y) \end{equation} の関係を使って、関数の合成を行うと \(z\) 平面上の関数と見ることもできる: \begin{equation} \psi \bigl( f(z) \bigr) = \phi\bigl( u(x,y),v(x,y) \bigr) \, + \, i \chi \bigl( u(x,y),v(x,y) \bigr) \end{equation} この正則関数同士の合成関数 \(\psi(f(z))\) は再び正則関数となり、コーシー・リーマンの微分方程式 \begin{equation} \frac{\d\phi}{\d x} = \frac{\d\chi}{\d y}, \4 \frac{\d\phi}{\d y} = -\frac{\d\chi}{\d x} \end{equation} を満足する。実際、式\eqref{cauchy}や式\eqref{cauchy2}を利用すると \begin{align*} \frac{\d\phi}{\d x} &= \biggl( \frac{\d\phi}{\d u} \frac{\d u}{\d x} + \frac{\d\phi}{\d v} \frac{\d v}{\d x} \biggr) = \biggl( \frac{\d\chi}{\d v} \frac{\d v}{\d y} + \Bigl( -\frac{\d\chi}{\d u} \Bigr) \Bigl( -\frac{\d u}{\d y} \Bigr) \biggr) = \frac{\d\chi}{\d y} \\[5pt] \frac{\d\phi}{\d y} &= \biggl( \frac{\d\phi}{\d u} \frac{\d u}{\d y} + \frac{\d\phi}{\d v} \frac{\d v}{\d y} \biggr) = \biggl( \frac{\d\chi}{\d v} \, \Bigl( -\frac{\d v}{\d x} \Bigr) + \Bigl( -\frac{\d\chi}{\d u} \Bigr) \, \frac{\d u}{\d x} \biggr) = -\frac{\d\chi}{\d x} \end{align*} である。先ほども述べたように、コーシー・リーマンの微分方程式を満足する一対の実関数はいずれもラプラス方程式を満足するので、とくに \(\phi(u(x,y),v(x,y))=V(x,y)\) はラプラス方程式 \begin{equation} \biggl( \frac{\d^{2}}{\d x^{2}} + \frac{\d^{2}}{\d y^{2}} \biggr) \, \phi \bigl( u(x,y), v(x,y) \bigr) = 0 \end{equation} を満足することになる。これがもともと示したかった式\eqref{laplace3}である。

次に \(V(x,y)\) が3つの境界条件を満足していることを見ていこう。まず、式\eqref{boundary2}が成り立つならば式\eqref{boundary5}が成り立つこと、すなわち \(uv\)-平面にある物質と電極の境界(4か所)において \begin{equation} \phi = \text{一定} \end{equation} であるならば、\(xy\)-平面にある物質と電極の境界(4か所)においても \begin{equation} V = \text{一定} \end{equation} となることを言う。この条件は、電極を点電極と考える場合にはトリビアルな条件で、その一定値(というか1点での値)は両平面に共通で \begin{equation} V_{\mr{A}} = \phi_{\mr{P}}^{\,}, \3 V_{\mr{B}} = \phi_{\mr{Q}}^{\,}, \3 V_{\mr{C}} = \phi_{\mr{R}}^{\,}, \3 V_{\mr{D}} = \phi_{\mr{S}}^{\,} \end{equation} となる(電極はシート状物質の厚さ方向に長さをもっていてよいので、点電極でなく線電極と呼ぶほうが正確だろうか)。現実的には、各電極は \(0\) でない有限の面積をもっており、その意味で van der Pauw 法は近似的な測定手法となるだろう。式\eqref{phiuv}の \(\phi(u,v)\) は点電極の場合における厳密解なので、van der Pauw 法が数学的に完全な厳密性を有するのは、物質に取り付けられた4つの電極の大きさが無限小となる場合だけである。
残りの2つの境界条件はまとめて考えてしまう。証明したいのは、\(uv\)-平面において \begin{align} \nabla &\phi \cdot \bm{n} = 0 & &\text{(物質とまわりの空間の境界面上において)} \\[5pt] \int_{S_{W}^{\,}} \nabla \phi &\cdot \bm{n} \, dS = \frac{I_{W}}{\sigma} & &\text{(\(\,W=\mr{P},\mr{Q},\mr{R},\mr{S}\,\))} \end{align} であるならば、\(xy\)-平面においても \begin{align} \nabla &V \cdot \bm{n} = 0 & &\text{(物質とまわりの空間の境界面上において)} \\[5pt] \int_{S_{Z}^{\,}} \nabla V &\cdot \bm{n} \, dS = \frac{I_{Z}}{\sigma} & &\text{(\(\,Z=\mr{A},\mr{B},\mr{C},\mr{D}\,\))} \end{align} が成り立つことである。これを示すためにまず次のような微分量を考える: \begin{equation} \nabla V \cdot \bm{n} \, dS \end{equation} ただし \(\bm{n}\) は物質の表面外側に立てた単位法線ベクトル、\(dS\) はその点における微小面積要素である。この式をこのままベクトルの形式で扱ってもよいのだが、せっかく上で複素平面を導入したのだから、ここでは複素数を使った証明をしてみよう。2次元平面内の空間ベクトルは、直交座標系の単位ベクトル \((\bm{e}_{x},\bm{e}_{y})\) を \begin{equation} \bm{e}_{x} \to 1, \3 \bm{e}_{y} \to i \end{equation} と読みかえることにより複素平面上に置かれた複素数と同一視できる。例えば \(\nabla V\) というベクトルは \begin{equation} \nabla V = \bm{e}_{x} \frac{\d V}{\d x} + \bm{e}_{y} \frac{\d V}{\d y} \ \longrightarrow \ \frac{\d V}{\d x} + i \frac{\d V}{\d y} \end{equation} のような複素数へ読みかえられる。同様にして \(\bm{n}\,dS\) というベクトルを複素数で表したい。そのために物質の境界上に、境界および \(xy\)-平面に平行な線素ベクトル \begin{equation} d\bm{s} = \bm{e}_{x} \, dx + \bm{e}_{y} \, dy \end{equation} を取る。これは複素数で表すと \begin{equation} d\bm{s} \ \to \ dz = dx + i \, dy \end{equation} になる。ここで \(d\bm{s}\) の向きを常に物質を左手に見ながら進む向きと定義することにすると、\(\bm{n}\) の向きは \(d\bm{s}\) を平面内で \(-90^{\circ}\) 回転させた方向となるから、結局 \(\bm{n}\,dS\) というベクトルを複素数で表現したものは \begin{equation} \bm{n} \, dS \ \to \ -i \1 dz \, dt \end{equation} という形になる。ただし \(dt\) は物質の厚さ方向の微小長さである。次にベクトルの内積を複素数形式で表現したい。2つのベクトル \(\bm{a}=a_{x}\,\bm{e}_{x}+a_{y}\,\bm{e}_{y}\) と \(\bm{b}=b_{x}\,\bm{e}_{x}+b_{y}\,\bm{e}_{y}\) の内積は \begin{equation} \bm{a} \cdot \bm{b} = a_{x} b_{x} + a_{y} b_{y} \end{equation} であるが、これと同じ量は2つの複素数 \(a=a_{x}+ia_{y},\ b=b_{x}+ib_{y}\) を使って \begin{align*} \Re ( \bar{a} \2 b ) &= \Re \bigl( ( a_{x} - i a_{y} ) ( b_{x} + i b_{y} ) \bigr) \\[3pt] &= \Re \bigl( ( a_{x} b_{x} + a_{y} b_{y} ) + i ( a_{x} b_{y} - a_{y} b_{x} ) \bigr) \\[3pt] &= a_{x} b_{x} + a_{y} b_{y} \end{align*} と作ることができる。したがって \(\nabla V\cdot\bm{n}\,dS\) という量は複素数を使って \begin{equation} \nabla V \cdot \bm{n} \, dS = \Re \biggl( \Bigl( \frac{\d V}{\d x} - i \frac{\d V}{\d y} \Bigr) ( -i \1 dz \, dt ) \biggr) \label{eq} \end{equation} と表現できることがわかった。
さて、上の式は \(x,y\) や \(V(x,y)\) を使って書かれているので \(z\) 平面の座標を使った表式である。ところが \(z\) 平面と \(w\) 平面は正則関数による座標変換 \begin{equation} w = f(z) = u(x,y) + i v(x,y) \end{equation} によってつながっているのだから、式\eqref{eq}は \(w\) 平面の座標 \(u,v\) や電位 \(\phi(u,v)\) を使って表すこともできるはずである(次の計算では \(V(x,y)=\phi(u,v)\) に注意): \begin{align} \nabla V \cdot \bm{n} \, dS &= \Re \biggl( \Bigl( \frac{\d V}{\d x} - i \frac{\d V}{\d y} \Bigr) ( -i \1 dz \, dt ) \biggr) \notag \\[3pt] &= \Re \biggl( \biggl( \Bigl( \frac{\d \phi}{\d u} \frac{\d u}{\d x} + \frac{\d \phi}{\d v} \frac{\d v}{\d x} \Bigr) - i \Bigl( \frac{\d \phi}{\d u} \frac{\d u}{\d y} + \frac{\d \phi}{\d v} \frac{\d v}{\d y} \Bigr) \biggr) \biggl( -i \frac{dz}{dw} dw \, dt \biggr) \biggr) \notag \\[3pt] &= \Re \biggl( \frac{1}{dw/dz} \biggl( \Bigl( \frac{\d u}{\d x} + i \frac{\d v}{\d x} \Bigr) \frac{\d \phi}{\d u} - \Bigl( \frac{\d u}{\d y} + i \frac{\d v}{\d y} \Bigr) \frac{\d \phi}{\d v} \biggr) ( -i \1 dw \, dt ) \biggr) \label{eq2} \end{align} ただし、計算の途中でコーシー・リーマンの微分方程式 \begin{equation} \frac{\d u}{\d x} = \frac{\d v}{\d y}, \4 \frac{\d u}{\d y} = -\frac{\d v}{\d x} \end{equation} を利用した。ところで、複素関数 \(w=f(z)\) がある点 \(z_{0}\) で微分可能であるとは、\(z_{0}\) へ近づく方向によらず微分係数が一定の値をもつという意味であった。そのため微分可能な複素関数の微分係数を求めたい場合には、\(x\) 軸と平行 \((z=iy)\) に移動して偏微分しても、\(y\) 軸と平行 \((z=x)\) に移動して偏微分しても結果は同じとなり、したがって正則関数 \(w=f(z)=u(x,y)+iv(x,y)\) の導関数に関して \begin{equation} \frac{dw}{dz} = \Bigl( \frac{\d u}{\d x} + i \frac{\d v}{\d x} \Bigr) = \frac{1}{i}\Bigl( \frac{\d u}{\d y} + i \frac{\d v}{\d y} \Bigr) \end{equation} が成り立つ。これより式\eqref{eq2}は \begin{equation} \nabla V \cdot \bm{n} \, dS = \Re \biggl( \Bigl( \frac{\d\phi}{\d u} - i \frac{\d\phi}{\d v} \Bigr) ( -i \1 dw \, dt ) \biggr) \end{equation} となるのだが、式\eqref{eq}を参考にして、これをベクトル形式に戻すと最終的に \begin{equation} \nabla_{z} \2 V \cdot \bm{n}_{z} \, dS_{z} = \nabla_{w} \2 \phi \cdot \bm{n}_{w} \, dS_{w} \label{eq3} \end{equation} という結果を得る。ただし、どちらの座標平面で測った量であるかが明確になるように \(z\) や \(w\) という添字を付けた。
ここまで来てしまえばあとは簡単である。もし \(w\) 平面の境界面上のある点で \(\nabla\phi\cdot\bm{n}=0\) が成立しているのであれば、\(w=f(z)\) によって対応する \(z\) 平面上の点(それはやはり境界にある)においても \(\nabla V\cdot\bm{n}=0\) が成立していなければならない \((\because dS\neq0)\) 。このことより \(V(x,y)\) が境界条件の1つ目を満足していることがわかる。また、式\eqref{eq3}を電極と物質の境界上で面積分すれば \begin{equation} \int_{S_{Z}} \nabla_{z} \2 V \cdot \bm{n}_{z} \, dS_{z} = \int_{S_{W}} \nabla_{w} \2 \phi \cdot \bm{n}_{w} \, dS_{w} = \frac{I_{W}}{\sigma} \end{equation} という式が得られるので、\(I_{Z}=I_{W}\) であれば(\(\,z\) 平面と \(w\) 平面で同じ大きさの電流を流すならば)、最後の境界条件も満足されることになる。以上で \(V(x,y)=\phi(u(x,y),v(x,y))\) という関数がラプラス方程式と境界条件をすべて満足していることが示された。
付録 共役調和関数
ラプラス方程式 \(\nabla^{2}\phi=0\) を満たす関数を調和関数という。また、とくに2次元の平面上でのラプラス方程式 \begin{equation} \biggl( \frac{\d^{2}}{\d x^{2}} + \frac{\d^{2}}{\d y^{2}} \biggr) \phi(x,y) = 0 \label{laplace4} \end{equation} を満足するような調和関数 \(\phi(x,y)\) が与えられたとき、コーシー・リーマンの微分方程式 \begin{equation} \frac{\d\phi}{\d x} = \frac{\d\chi}{\d y}, \4 \frac{\d\phi}{\d y} = -\frac{\d\chi}{\d x} \label{cauchy3} \end{equation} を満たすような関数 \(\chi(x,y)\) を、\(\phi(x,y)\) の共役調和関数という。コーシー・リーマンの微分方程式より、\(\chi(x,y)\) もラプラス方程式を満足することになるのだが、実はこのような \(\chi(x,y)\) は定数のちがいを除いて一意的に決まってしまう。以下では \(\phi(x,y)\) に具体的な関数形を与えた上で、実際にそのような \(\chi(x,y)\) が構成可能なことを見ていこう。
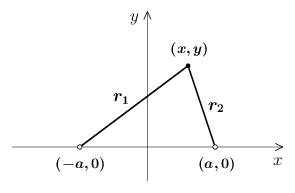
上半平面 \(y\gt0\) で定義された実関数 \begin{equation} \phi(x,y) = \ln \Bigl( \frac{r_{2}}{r_{1}} \Bigr) = \ln \sqrt{\frac{(x-a)^{2}+y^{2}}{(x+a)^{2}+y^{2}}} \label{phi2} \end{equation} の共役調和関数 \(\chi(x,y)\) を求めたい(計算は省略するが \(\phi(x,y)\) はラプラス方程式を満足している)。まず \(\phi(x,y)\) を \(x\) で偏微分すると \begin{align*} \frac{\d\phi}{\d x} &= \frac{1}{2} \frac{\d}{\d x} \Bigl( \ln \bigl( (x-a)^{2} + y^{2} \bigr) - \ln \bigl( (x+a)^{2} + y^{2} \bigr) \Bigr) \\[5pt] &= \frac{x-a}{(x-a)^{2}+y^{2}} - \frac{x+a}{(x+a)^{2}+y^{2}} \end{align*} になるから、コーシー・リーマンの微分方程式\eqref{cauchy3}より、これを \(y\) で積分したものが \(\chi(x,y)\) である: \begin{equation*} \chi(x,y) = \int \biggl( \frac{x-a}{(x-a)^{2}+y^{2}} - \frac{x+a}{(x+a)^{2}+y^{2}} \biggr) \, dy \end{equation*} ここで積分公式 \begin{equation} \int \frac{x'}{x'^{2}+y^{2}} \, dy = \Atan \Bigl( \frac{y}{x'} \Bigr) + C \5 \Bigl( -\frac{\pi}{2} \lt \Atan(\cdot) \lt \frac{\pi}{2} \Bigr) \end{equation} を利用すれば(「不定積分の公式」参照)、計算結果は次のようになる: \begin{equation} \chi(x,y) = \Atan \Bigl( \frac{y}{x-a} \Bigr) - \Atan \Bigl( \frac{y}{x+a} \Bigr) + X(x) \label{chi} \end{equation} ただし \(X(x)\) は \(x\) だけの関数で積分定数に相当する。この未定関数 \(X(x)\) を決定するにはコーシー・リーマンの微分方程式\eqref{cauchy3}のもう1つ \begin{equation} \frac{\d\phi}{\d y} = -\frac{\d\chi}{\d x} \label{cauchy4} \end{equation} を使えばよい。関数 \(\phi(x,y)\) を \(y\) で偏微分すると \begin{equation} \frac{\d\phi}{\d y} = \frac{y}{(x-a)^{2}+y^{2}} - \frac{y}{(x+a)^{2}+y^{2}} \end{equation} となり、一方で式\eqref{chi}の \(\chi(x,y)\) を \(x\) で偏微分すると \begin{equation} \frac{\d\chi}{\d x} = -\frac{y}{(x-a)^{2}+y^{2}} + \frac{y}{(x+a)^{2}+y^{2}} + \frac{dX}{dx} \label{eq4} \end{equation} となるから、コーシー・リーマンの微分方程式\eqref{cauchy4}より \(dX/dx=0\)、すなわち \(X(x)\) は任意の定数である、という話になりそうなのだが、実はこの議論には少し間違いがある。というのも、式\eqref{eq4}で行った偏微分の計算には、その演算が定義されない点(の集合)が存在しているのである: 式\eqref{chi}で \(\Atan\) が定義されない \(x=\pm a,\ y\gt0\) だ。今の問題で最初に与えられた \(\phi(x,y)\) という関数は、上半平面 \(y\gt0\) の全体で定義されている関数だから、それに共役な \(\chi(x,y)\) も同じ領域で定義されるべきものである。また、それは当然コーシー・リーマンの微分方程式を満足するようなものでなければならず、そのため \(\chi(x,y)\) は、上半平面全体において \(x\) でも \(y\) でも偏微分可能な関数になっていなければならない。とくに \(x\) についての偏微分可能性は、\(\chi(x,y)\) が \(x\) について連続関数になっていることを要求する。ところが、式\eqref{chi}の \(\chi(x,y)\) は一見すると変数 \(x\) に関して連続関数になっていない。この問題をどのように解決すればよいだろうか?
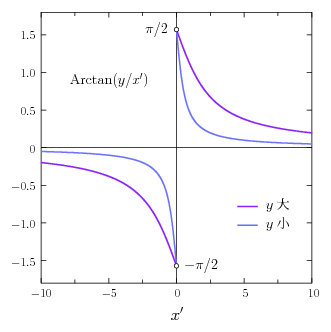
一般に、上半平面 \(y\gt0\) において、次の関数 \begin{equation} \Atan \Bigl( \frac{y}{x'} \Bigr) \end{equation} は \(x'=0\) となる点においてその値が定義されない(上図参照)。また、たとえ \(x'=0\) での値を適当に定めたとしても、それだけでこれを連続関数にすることはできない(\(\,x'=0\) での \(\Atan(y/x')\) の値を \(\pi/2\) と定義しても \(-\pi/2\) と定義してもダメである)。しかしながら、これを少し修正した \begin{equation} \Arg ( x' + iy ) = \begin{cases} \Atan (y/x') & ( x' \gt 0 ) \\[3pt] \pi/2 & ( x' = 0 ) \\[3pt] \Atan (y/x') + \pi & ( x' \lt 0 ) \end{cases} \end{equation} は上半平面全体で連続となる(記号の使い方から予想がつくと思うが、この関数は複素数 \(x'+iy\) の偏角の主値を返す)。もし \(x'=0\) で \(\Atan(y/x')=0\) と定義するなら、この関数を次のように表現することもできるだろう: \begin{equation} \Arg ( x' + iy ) = \Atan \Bigl( \frac{y}{x'} \Bigr) + \pi \1 H(-x') \end{equation} ただし \(H\) はヘヴィサイドの階段関数 \begin{equation} H(x) = \begin{cases} 0 & ( x \lt 0 ) \\[3pt] 1/2 & ( x = 0 ) \\[3pt] 1 & ( x \gt 0 ) \end{cases} \end{equation} を表す。また、\(\Arg(x'+iy)\) は上半平面全体 \((y\gt0)\) で \(x'\) でも \(y\) でも偏微分可能である: \begin{equation} \frac{\d}{\d x'} \,\Arg ( x' + iy ) = -\frac{y}{x'^{2}+y^{2}}, \4 \frac{\d}{\d y} \,\Arg ( x' + iy ) = \frac{x'}{x'^{2}+y^{2}} \end{equation} とくに \(x'=0\) において \(x'\) で偏微分可能なことは下に示したグラフから理解できるだろうか(実は \(\Atan(y/x')\) の偏導関数は最初から上半平面全体で定義可能な形をしていた)。これらの偏導関数はいずれも上半平面全体で連続だから \(\Arg(x'+iy)\) は上半平面全体で微分可能でもある。
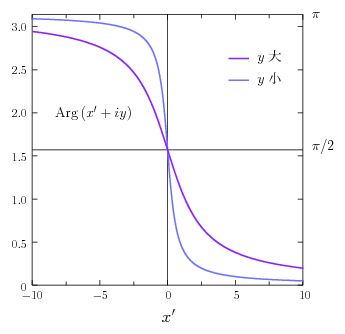
以上の一般論を踏まえて、式\eqref{chi}の中に現れる任意関数 \(X(x)\) を \begin{equation*} X(x) \ \longrightarrow \ \pi \1 H(-(x-a)) - \pi \1 H(-(x+a)) + X(x) \end{equation*} と置き直してみよう。このとき式\eqref{chi}は次のように書き換わる: \begin{align*} \chi(x,y) &= \Arg ( x - a + iy ) - \Arg ( x + a + iy ) + X(x) \\[5pt] &= \Arg ( z - a ) - \Arg ( z + a ) + X(x) \end{align*} ただし \(x+iy=z\) と置いた。こうなってしまえばあとは簡単で、\(\Arg(z\pm a)\) は上半平面全体で微分可能なのだから、式\eqref{cauchy4}から始まる議論は定義域の全体でそのまま間違いなく適用可能となり、最終的に \begin{equation} \chi(x,y) = \Arg ( z - a ) - \Arg ( z + a ) + C \label{chi2} \end{equation} を得る(\(\,C\) は定数)。ところで上半平面においては \begin{equation*} 0 \lt \Arg ( z - a ) \lt \pi, \4 0 \lt \Arg ( z + a ) \lt \pi \end{equation*} であるから、偏角の主値を \(-\pi\) から \(\pi\) までの範囲に選ぶことにすれば、上の \(\chi(x,y)\) は \begin{equation} \chi(x,y) = \Arg \Bigl( \frac{z-a}{z+a} \Bigr) + C \end{equation} と表してもよいことになる。
以上で \(\phi(x,y)\) の共役調和関数 \(\chi(x,y)\) が求まったことになるが、複素関数論の一般論により、コーシー・リーマンの微分方程式を満足する1組の関数はある正則関数の実部や虚部になっていなければならない。実際に \(\phi(x,y),\,\chi(x,y)\) の具体形を用いて \(\phi+i\chi\) という量を計算してみると \begin{align} \phi(x,y) + i \chi(x,y) &= \ln \sqrt{\frac{(x-a)^{2}+y^{2}}{(x+a)^{2}+y^{2}}} + i \1 \Arg \Bigl( \frac{x-a+iy}{x+a+iy} \Bigr) + C \notag \\[3pt] &= \ln \, \biggl| \frac{z-a}{z+a} \biggr| + i \1 \Arg \Bigl( \frac{z-a}{z+a} \Bigr) + C \notag \\[5pt] &= \Log \Bigl( \frac{z-a}{z+a} \Bigr) + C \end{align} となり \(\bar{z}\) を含まない \(z\) だけの関数が得られる。この関数は上半平面全体(\(\,\Im z\gt0\,\))で正則である。