定常電流

定常電流の基本方程式

定常電流は電磁気学の問題なので基本となる式はマクスウェル方程式 \begin{align} &\nabla \ip \bm{D} = \rho, & &\nabla \op \bm{E} = -\frac{\d\bm{B}}{\d t} \\[3pt] &\nabla \ip \bm{B} = 0, & &\nabla \op \bm{H} = \bm{i} + \frac{\d\bm{D}}{\d t} \end{align} である。定常電流というのは、例えば電池を使って物質に直流電圧を加えたとき、電気を流し始めた瞬間にはもちろん電流の時間的変動があるだろうが、その後に十分な時間が経過したあとの、物質に流れる電流が時間的に一定となった状態のことをいう。このような定常的な状態を考える場合には電場や磁場、電荷密度や電流密度はすべて時間によらず一定となるため、マクスウェル方程式からは時間微分の項が消えて \begin{align} &\nabla \ip \bm{D} = \rho, & &\nabla \op \bm{E} = 0 \\[8pt] &\nabla \ip \bm{B} = 0, & &\nabla \op \bm{H} = \bm{i} \end{align} となる。ところで、多くの物質では電場と電束密度、磁場と磁束密度の間に \begin{equation} \bm{D} = \varepsilon \bm{E}, \4 \bm{B} = \mu \bm{H} \end{equation} という関係式が成立していて（誘電率 \(\varepsilon\) や透磁率 \(\mu\) は定数）、この場合、マクスウェル方程式は電場 \(\bm{E}\) と磁束密度 \(\bm{B}\) だけを使って \begin{align} &\nabla \ip \bm{E} = \frac{\rho}{\varepsilon}, & &\nabla \op \bm{E} = 0 \label{ele} \\[5pt] &\nabla \ip \bm{B} = 0, & &\nabla \op \bm{B} = \mu \1 \bm{i} \label{mag} \end{align} と表すことができる。また、オームの法則 \begin{equation} \bm{i} = \sigma \bm{E} \label{ohm} \end{equation} も多くの物質において成立することが知られている。ただし、定数 \(\sigma\) は電気伝導率（導電率）である。さて、ここで式\eqref{mag}の右側（アンペールの法則）の発散を取ってみよう。\(\nabla\ip(\nabla\op\bm{B})=0\) が恒等的に成り立つことに注意すると \begin{equation} \nabla \cdot \2 \bm{i} = 0 \label{current} \end{equation} を得る。これは定常電流の保存を表す式で、連続の方程式 \begin{equation} \frac{\d\rho}{\d t} + \nabla \cdot \2 \bm{i} = 0 \end{equation} の特別な場合となっている。定常電流の保存則に注意してオームの法則\eqref{ohm}の発散を取ると \begin{equation} \nabla \ip \bm{E} = 0 \end{equation} という式になるが、これを式\eqref{ele}の左側（ガウスの法則）と比較すると \begin{equation} \rho = 0 \end{equation} でなければならないとわかる。すなわち、オームの法則が成立し、定常的な電流が流れている状況において電荷分布の存在は許されない。

ここまでの結果をまとめると次のようになる： \begin{equation} \nabla \ip \bm{E} = 0, \3 \nabla \op \bm{E} = 0 \ \ \2 \label{ele2} \end{equation} \begin{equation} \nabla \ip \bm{B} = 0, \3 \nabla \op \bm{B} = \mu \1 \bm{i} \label{mag2} \end{equation} \begin{equation} \bm{i} = \sigma \bm{E} \label{ohm2} \end{equation} これらの式の構造を見ていくと、まず式\eqref{ele2}の2つは静電場 \(\bm{E}\) を決定するための方程式になっている。この方程式を解いて静電場が決定されたなら、オームの法則\eqref{ohm2}を用いることで電流密度 \(\bm{i}\) も直ちに得られる。そして、その電流密度を使って方程式\eqref{mag2}を解くことで、電流が生み出した静磁場も決定されることになる。しかし、この先でとくに考察したいのは電流の分布だけなので、静磁場を求める式\eqref{mag2}は必要にならない。この式は磁場の様子まで知りたいときに使うオマケのようなものである。

それでは静電場の方程式\eqref{ele2}を解くことを考えよう。よく知られているように、あるベクトル場の回転が恒等的に \(0\) である場合、そのベクトル場はスカラー値のポテンシャル関数の勾配として表すことができる。今の場合 \(\nabla\op\bm{E}=0\) という式が成立しているので、静電場 \(\bm{E}\) はスカラーポテンシャル \(\phi\) を使って \begin{equation} \bm{E} = -\nabla \phi \end{equation} と表すことができる。そしてこの表現を式\eqref{ele2}の左側（ガウスの法則）に代入すれば、ラプラスの方程式 \begin{equation} \nabla^{2} \phi = 0 \label{laplace} \end{equation} を得る。結局、定常電流を求める問題というのは、適当な境界条件の下でラプラス方程式を解くという問題に帰着する。ラプラス方程式を解いてスカラーポテンシャルを求めることさえできてしまえば、あとは \begin{equation} \bm{i} = -\sigma \2 \nabla \phi \label{ohm3} \end{equation} を計算するだけで所望の電流密度が得られることになる。

ラプラス方程式の境界条件と解の一意性

ラプラス方程式\eqref{laplace}はシンプルな形をした方程式であるが、2階の偏微分方程式であるため、多くの場合、これを解くことは非常に難しい（解析的にも、数値的にも）。ここでは定常電流の問題を具体的に解き始める前に、ラプラス方程式の解が持つべき一般的性質についてまず調べていくことにする。境界条件としては定常電流の問題を想定したものを考える。

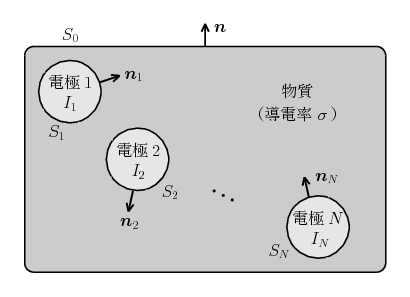
上の図のように、有限の導電率 \(\sigma\) をもった物質上に \(N\) 個の金属電極が取り付けられている状況を考えよう。各電極には直流電源が接続され、\(k\) 番目の電極からは一定の電流 \(I_{k}\) が物質中へ流れ出している。そして、この電流値は電流計で測定するなどしてあらかじめわかっているものとしよう。このとき物質中に生じる電流密度の分布 \(\bm{i}\) は、ラプラス方程式\eqref{laplace}とオームの法則\eqref{ohm3}から決定されることになるが、実際にはこれら2つの式だけでは不十分である。微分方程式を解くためには境界条件も同時に与えなければならない。今求めたいのは物質中を流れる電流密度なので、境界とは、物質とそれ以外の空間の境目のことである。上の図の状況では、物質とその外側の何もない空間の境界面 \(S_{0}\)、および物質と電極のあいだの境界面 \(S_{k}\ (k=1,2,\dots,N)\) のことである。これらの境界において、電流密度 \(\bm{i}\) や電位（スカラーポテンシャル）\(\phi\) にはどのような条件が課されるだろうか？ まず物質とその外側の何もない空間の境界において、そこへ流出する電流やそこから流入してくる電流は \(0\) になるだろう（現実的には、物質が置かれた絶縁性の実験台や、物質のまわりにある空気の層などが外側の空間に相当し、実質的にその導電率は \(\sigma=0\) と考えてよい）。よって、物質の表面外側に立てた単位法線ベクトルを \(\bm{n}\) と書けば、物質とその外側の何もない空間の境界において \begin{equation} \bm{i} \cdot \bm{n} = 0 \4 \text{（\(\,S_{0}\) 上において）} \label{boundarya} \end{equation} が言える。これはオームの法則\eqref{ohm3}を使って \begin{equation} \nabla \phi \cdot \bm{n} = 0 \4 \text{（\(\,S_{0}\) 上において）} \end{equation} と表してもよい。次に電極 \(k\) と物質のあいだの境界面 \(S_{k}\) を考える。今、金属電極は理想的な金属でできているものとし、その導電率は \(\infty\) であるとしよう。この場合、金属電極 \(k\) 上の電位は場所によらず一定値を取るから、とくに物質との境界面において \begin{equation} \phi = \text{一定} \4 \text{（\(\,S_{k}\) 上において）} \end{equation} が言える。この一定値がいくらになるかは実際にラプラス方程式を解いてみないとわからないのだが、一般には、各電極ごとに異なった一定値となることに注意しておこう。さて、電極 \(k\) から流れ出す電流は \(I_{k}\) であったから、電極 \(k\) の表面 \(S_{k}\) 上で電流密度を面積分すると \begin{equation} \int_{S_{k}} \bm{i} \cdot \bm{n}_{k} \, dS = I_{k} \5 \text{（\(\,k=1,2,\dots,N\,\)）} \label{boundaryb} \end{equation} という条件も得られる（ただし \(\bm{n}_{k}\) は電極 \(k\) の表面外側に立てた単位法線ベクトル）。物質と電極の境界面である \(S_{k}\) 上においては、電極の表面外側に立てた単位法線ベクトル \(\bm{n}_{k}\) と、物質の表面外側に立てた単位法線ベクトル \(\bm{n}\) の間に \(\bm{n}_{k}=-\bm{n}\) という関係が成立すること、およびオームの法則\eqref{ohm3}を使うと、式\eqref{boundaryb}は \begin{equation} \int_{S_{k}} \nabla \phi \cdot \bm{n} \, dS = \frac{I_{k}}{\sigma} \5 \text{（\(\,k=1,2,\dots,N\,\)）} \end{equation} と表すこともできる。

ここまでをまとめると、定常電流の問題におけるラプラス方程式 \begin{equation} \nabla^{2} \phi = 0 \label{laplace2} \end{equation} の境界条件は \begin{equation} \nabla \phi \cdot \bm{n} = 0 \4 \text{（\(\,S_{0}\) 上において）} \label{boundary1} \end{equation} \begin{equation} \phi = \text{一定} \5 \, \text{（\(\,S_{k}\) 上において）} \label{boundary2} \end{equation} \begin{equation} \int_{S_{k}} \nabla \phi \cdot \bm{n} \, dS = \frac{I_{k}}{\sigma} \4 \text{（\(\,k=1,2,\dots,N\,\)）} \label{boundary3} \end{equation} で与えられることになる。ところで、これらの境界条件を満足するようなラプラス方程式の解が1つ求まったとして、その解は本当に現実の現象を再現するようなただ一つの解になるだろうか。もしかしたら、上で与えた3つの境界条件だけでは解を一義的に決定するには十分でないかもしれず、そのような場合には任意関数が残るなどして解がただ一つに決まらない可能性もある。以下この節では、ラプラス方程式の解の一意性について考察していこう。

今、ラプラス方程式\eqref{laplace2}と境界条件\eqref{boundary1}-\eqref{boundary3}を満足するような異なる2つの解 \(\phi_{1}\) と \(\phi_{2}\) が見つかったとする（ただしこれらが各電極上で取る値は、それが一定でありさえすれば、たとえ同一の電極であったとしても \(\phi_{1}\) と \(\phi_{2}\) で異なる値となってもよい）。このとき新しい関数 \(\psi\) を \begin{equation} \psi = \phi_{1} - \phi_{2} \label{psi} \end{equation} で定義すると、\(\phi_{1}\) と \(\phi_{2}\) がいずれも式\eqref{laplace2}-\eqref{boundary3}を満足することより、その重ね合わせ \(\psi\) もラプラス方程式 \begin{equation} \nabla^{2} \psi = 0 \label{laplace3} \end{equation} を満たす。ただし \(\psi\) が満足すべき境界条件は3番目が少し違っていて \begin{equation} \nabla \psi \cdot \bm{n} = 0 \4 \text{（\(\,S_{0}\) 上において）} \label{boundary4} \end{equation} \begin{equation} \psi = \text{一定} \5 \, \text{（\(\,S_{k}\) 上において）} \label{boundary5} \end{equation} \begin{equation} \int_{S_{k}} \nabla \psi \cdot \bm{n} \, dS = 0 \4 \text{（\(\,k=1,2,\dots,N\,\)）} \label{boundary6} \end{equation} という形になる。さて、ガウスの発散定理 \begin{equation} \int_{V} \nabla \ip \bm{A} \, dV = \int_{\d V} \bm{A} \ip \bm{n} \, dS \end{equation} において、\(\bm{A}=\psi\,\nabla\psi\) と置き、また積分領域を物質内全体にしてみよう： \begin{equation} \int_{\text{物質内}} \nabla \ip ( \psi \, \nabla \psi ) \, dV = \int_{\text{物質表面}} \psi \, \nabla \psi \cdot \bm{n} \, dS \label{eq} \end{equation} ここで、左辺の体積積分は、ラプラス方程式\eqref{laplace3}を利用すると \begin{equation*} \int_{\text{物質内}} \nabla \ip ( \psi \, \nabla \psi ) \, dV = \int_{\text{物質内}} \Bigl( ( \nabla \psi )^{2} + \psi \, \nabla^{2} \psi \Bigr) \, dV = \int_{\text{物質内}} ( \nabla \psi )^{2} \, dV \end{equation*} のように変形される。また、面積分の方は \begin{align*} \int_{\text{物質表面}} \psi \, \nabla \psi \cdot \bm{n} \, dS &= \int_{S_{0}} \psi \, \nabla \psi \cdot \bm{n} \, dS + \sum_{k=1}^{N} \biggl( \int_{S_{k}} \psi \, \nabla \psi \cdot \bm{n} \, dS \biggr) \\[5pt] &= \int_{S_{0}} \psi \, ( \nabla \psi \cdot \bm{n} ) \, dS + \sum_{k=1}^{N} \psi \biggl( \int_{S_{k}} \nabla \psi \cdot \bm{n} \, dS \biggr) \end{align*} と変形できる。ただし \(S_{k}\) 上の積分では、境界条件\eqref{boundary5}によって電極上で \(\psi\) が一定となることより \(\psi\) を積分の前に出した。この式に境界条件の式を用いると、式\eqref{boundary4}より第1項は \(0\)、また式\eqref{boundary6}より第2項も \(0\) になる。したがって、式\eqref{eq}は \begin{equation*} \int_{\text{物質内}} ( \nabla \psi )^{2} \, dV = 0 \end{equation*} ということになるが、\((\nabla\psi)^{2}\ge0\) であるから、この体積積分が等号で成り立つためには物質内のすべての点で \begin{equation*} \nabla \psi = 0 \end{equation*} が成立していなければならない。すなわち \(\psi\) は物質内において定数であり、式\eqref{psi}から \begin{equation} \phi_{1} - \phi_{2} = \text{定数} \end{equation} が結論される。ゆえに、境界条件\eqref{boundary1}-\eqref{boundary3}の下で解かれたラプラス方程式の解は、定数分の不定性を除いて一義的に定まることになる。この定数分の不定性は、電位の基準をどこにするかという任意性から来るものであり、例えば \(N\) 個ある電極のうちの1つについて、その電位を \(0\) と決めてしまえばこの不定性は解消される（通常は回路のグランドに接続されている電極をそのような基準電極として選ぶ）。

重ね合わせの原理

ここまで見てきたように、ラプラス方程式 \begin{equation} \nabla^{2} \phi = 0 \label{laplace4} \end{equation} を境界条件 \begin{equation} \nabla \phi \cdot \bm{n} = 0 \4 \text{（\(\,S_{0}\) 上において）} \label{boundary7} \end{equation} \begin{equation} \phi = \text{一定} \5 \, \text{（\(\,S_{k}\) 上において）} \label{boundary8} \end{equation} \begin{equation} \int_{S_{k}} \nabla \phi \cdot \bm{n} \, dS = \frac{I_{k}}{\sigma} \4 \text{（\(\,k=1,2,\dots,N\,\)）} \label{boundary9} \end{equation} の下で解けば、その解は任意定数の不定性を除いて一意的に定まる。とくに \(N\) 個ある電極のうちのいずれか1つの電位をある一定値に決めてしまえば \(\phi\) は完全に一意的となる。この節では \(N\) 番目の電極における電位を \(0\) と決め、定数分の不定性もなく \(\phi\) がただ1つに定まっている状況を考えることにしよう。

電位 \(\phi\) は物質内にとった空間座標 \(\bm{r}\) の関数であるが、境界条件\eqref{boundary9}より電流 \(I_{k}\) の大きさによってもその関数形は変わる。実際にラプラス方程式を解く場合には、各 \(I_{k}\) を定数として計算するのだが、今、一時的に \(I_{k}\) を自由に変えられる変数のように考えて \begin{equation} \phi = \varPhi(\bm{r},\,I_{1},\dots,I_{N}) \end{equation} と明示的に表示することにしよう。もし流す電流の大きさを変えれば電位の関数形も \begin{equation} \phi' = \varPhi(\bm{r},\,I'_{1},\dots,I'_{N}) \end{equation} のように形が変わる。ここで注意したいのは、\(\phi\) と \(\phi'\) は空間座標 \(\bm{r}\) の関数として異なる形をしているのだが、多変数関数 \(\varPhi\) の関数形は両者で共通となっていることである。ところで、物質に流す電流を \(I_{1}+I'_{1},\dots,I_{N}+I'_{N}\) に変化させたとき、電位 \begin{equation} \phi'' = \varPhi(\bm{r},\,I'_{1}+I'_{1},\dots,I'_{N}+I'_{N}) \end{equation} にはどのようなことが言えるだろうか？ 実は \begin{equation} \phi'' = \phi + \phi' \end{equation} となるのである。これを確認してみよう。確かめるには、\(\phi''=\phi+\phi'\) が電流を \(I_{1}+I'_{1},\dots,I_{N}+I'_{N}\) にしたときの境界条件を満足するラプラス方程式の解になっていることを言えばよい。まず、ラプラス方程式を満足していることはほとんど明らかで \begin{equation*} \nabla^{2} \phi'' = \nabla^{2} ( \phi + \phi' ) = \nabla^{2} \phi + \nabla^{2} \phi' = 0 \end{equation*} となるからよい。1つ目の境界条件\eqref{boundary7}についても同様である。2つ目の境界条件\eqref{boundary8}についても同様であるが、とくに電位の基準とした \(N\) 番目の電極に関して \begin{equation*} \phi'' = \phi + \phi' = 0 + 0 = 0 \4 \text{（\(\,S_{N}\) 上において）} \end{equation*} となっていることに注意しよう。3つ目の境界条件\eqref{boundary9}は電流 \(I_{k}\) を含んでいることに注意が必要だが、確認は同様に簡単で \begin{equation*} \int_{S_{k}} \nabla \phi'' \cdot \bm{n} \, dS = \int_{S_{k}} \nabla \phi \cdot \bm{n} \, dS + \int_{S_{k}} \nabla \phi' \cdot \bm{n} \, dS = \frac{(I_{k}^{\,}+I'_{k})}{\sigma} \end{equation*} となることからよい。以上によって \(\phi''\) が境界条件を満足するラプラス方程式の解になっていることが確かめられ、定常電流の問題において \begin{equation} \varPhi(\bm{r},\,I'_{1}+I'_{1},\dots,I'_{N}+I'_{N}) = \varPhi(\bm{r},\,I_{1},\dots,I_{N}) + \varPhi(\bm{r},\,I'_{1},\dots,I'_{N}) \end{equation} という式が成り立つことがわかった。これを重ね合わせの原理という。なお、物質に何も電流が流れていない場合には、とくに \begin{equation*} \varPhi(\bm{r},\,0,\dots,0) = \varPhi(\bm{r},\,0,\dots,0) + \varPhi(\bm{r},\,0,\dots,0) \end{equation*} という式が成り立たなければならないので \begin{equation} \varPhi(\bm{r},\,0,\dots,0) = 0 \end{equation} となることから、物質全体の電位が基準電極と同じ \(0\) になる。

ラプラス方程式の解法の具体例

以上の一般論を踏まえて、定常電流の問題を具体的に解いてみよう。

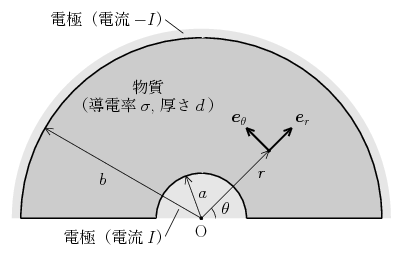
上の図のような半円形の一様なシート状物質（導電率 \(\sigma\)、厚さ \(d\,\)）に定常電流を流すことを考える。電極の1つは半円状物質の中心部分に半径 \(a\)、厚さ \(d\) で取り付けられており、ここから大きさ \(I\) の電流を流す。この陽極を出た電流は物質内を流れ、その外側に取り付けられた陰極（内径 \(b\)、厚さ \(d\)、外径はとくに必要ないのでいくつであってもよい）から物質の外へ出ていく。

さて、解くべきはラプラス方程式 \begin{equation} \nabla^{2} \phi = 0 \end{equation} であるが、この問題では系の対称性から考えて円柱座標系を用いるのが便利だろう。円柱座標 \((r,\theta,z)\) を採用するとき、電位 \(\phi\) が定義される領域は物質内の \begin{equation} a \le r \le b, \4 0 \le \theta \le \pi, \4 0 \le z \le d \end{equation} という範囲になる。また円柱座標で表現したラプラス方程式は \begin{equation} \biggl( \frac{\d^{2}}{\d r^{2}} + \frac{1}{r} \frac{\d}{\d r} + \frac{1}{r^{2}} \frac{\d^{2}}{\d\theta^{2}} + \frac{\d^{2}}{\d z^{2}} \biggr) \phi = 0 \end{equation} という形になる。今、シート状物質は一様であるから、厚さ方向（\(\,z\) 方向）には電位が変化しない2次元系と見なす（この取り扱いが正しいことは真面目な計算によっても示すことができるが、あまり難しい計算でなく、式が長くなるだけなので省略する）。このとき \(\phi=\phi(r,\theta)\) という形になり、ラプラス方程式は \begin{equation} \biggl( \frac{\d^{2}}{\d r^{2}} + \frac{1}{r} \frac{\d}{\d r} + \frac{1}{r^{2}} \frac{\d^{2}}{\d\theta^{2}} \biggr) \phi = 0 \label{laplace5} \end{equation} となる。この偏微分方程式を変数分離法によって解くため \begin{equation} \phi(r,\theta) = P(r) \2 Q(\theta) \end{equation} と置いて上の式へ代入すると \begin{equation*} Q(\theta) \biggl( \frac{d^{2}}{d r^{2}} + \frac{1}{r} \frac{d}{d r} \biggr) P(r) + \frac{P(r)}{r^{2}} \frac{d^{2}}{d\theta^{2}} Q(\theta) = 0 \end{equation*} または \begin{equation*} -\frac{r^{2}}{P(r)} \biggl( \frac{d^{2}}{d r^{2}} + \frac{1}{r} \frac{d}{d r} \biggr) P(r) = \frac{1}{Q(\theta)} \frac{d^{2}}{d\theta^{2}} Q(\theta) \end{equation*} となる。ここで左辺は \(r\) だけの関数、右辺は \(\theta\) だけの関数になっているから、この等式が \(r\) や \(\theta\) の値を任意に変化させたとしても恒等的に成立するためには \begin{equation} -\frac{r^{2}}{P(r)} \biggl( \frac{d^{2}}{d r^{2}} + \frac{1}{r} \frac{d}{d r} \biggr) P(r) = \frac{1}{Q(\theta)} \frac{d^{2}}{d\theta^{2}} Q(\theta) = k \, \text{（定数）} \end{equation} でないといけない。これにより1つの偏微分方程式が2つの常微分方程式に変わった。ここでは、まず \(Q(\theta)\) についての微分方程式を解いていくことにしよう： \begin{equation} \frac{d^{2}}{d\theta^{2}} Q(\theta) = k \, Q(\theta) \end{equation} この微分方程式の一般解は定数 \(k\) の符号によって次の3つに場合分けされる： \begin{equation} Q(\theta) = \begin{cases} C e^{n\theta} + D e^{-n\theta} & ( k = n^{2} \gt 0 ) \\[5pt] C \cos n \theta + D \sin n \theta \3 & ( k = -n^{2} \lt 0 ) \\[5pt] C + D \1 \theta & ( k = 0 ) \end{cases} \end{equation} ところが、極座標の偏角 \(\theta\) というのは \(2\pi\) の整数倍の不定性をもつ量であり、そのため \(Q(\theta)\) はその不定性に対して不変となるような周期的な関数になっていなければならない。それゆえ \(Q(\theta)\) として許されるのは、\(k=-n^{2}\lt0\) の場合における \begin{equation} Q(\theta) = C \cos n \theta + D \sin n \theta \label{eq2} \end{equation} という解と、\(k=0\) の場合でとくに \(D=0\) とした \begin{equation} Q(\theta) = C \label{eq3} \end{equation} という解だけである。式\eqref{eq2}は、よく見ると \(n=0\) と置くことで式\eqref{eq3}の場合を含んでいるから、これらの解をまとめて \begin{equation} Q(\theta) = C \cos n \theta + D \sin n \theta \5 ( n^{2} \ge 0 ) \end{equation} と書いてもよいだろう。\(Q(\theta)\) は周期 \(2\pi\) の周期関数となるべきであるから、\(Q(\theta+2\pi)=Q(\theta)\) より \begin{equation*} C \cos ( n \theta + 2\pi n) + D \sin ( n \theta + 2\pi n ) = C \cos n \theta + D \sin n \theta \end{equation*} が成り立たなければならず、そのため定数 \(n\) については条件 \begin{equation} n = 0, 1, 2, 3, \dots \end{equation} が要求される（\(\,n\) は負の整数であってもよいと考える人がいるかもしれないが、その場合の解は、任意定数 \(D\) を \(-D\) と書き直すことで、正の整数 \(|n|\) の場合における解とまったく同じ形にできるため考えなくてよい）。以上より \(Q(\theta)\) は \begin{equation} Q(\theta) = C \cos n \theta + D \sin n \theta \5 ( n = 0, 1, 2, 3, \dots ) \label{q} \end{equation} という形になることがわかった。

次に \(P(r)\) を求めてみよう。分離定数に \(k=-n^{2}\) という制限が付いたことにより解くべき微分方程式は \begin{equation} \biggl( \frac{d^{2}}{d r^{2}} + \frac{1}{r} \frac{d}{d r} - \frac{n^{2}}{r^{2}} \biggr) P(r) = 0 \5 ( n = 0, 1, 2, 3, \dots ) \label{eq4} \end{equation} となる。これをまじめに解いてもよいのだが、このくらいの微分方程式であれば見ただけで \(P(r)=r^{\alpha}\) という形の解を持ちそうだと予想できる（ただし \(\alpha\) は定数）。実際、\(P(r)=r^{\alpha}\) を上の式に代入すると \begin{equation*} \bigl( \alpha ( \alpha - 1 ) + \alpha - n^{2} \bigr) \, r^{n-2} = 0 \end{equation*} または \begin{equation*} \alpha^{2} = n^{2} \end{equation*} という2次方程式が得られるので \begin{equation} \alpha = n \3 \text{または} \3 \alpha = -n \end{equation} であれば \(r^{\alpha}\) は解になる。\(\alpha=n\) の場合と \(\alpha=-n\) の場合で2つの可能性が出てきてしまったが、一般的にはこれら2つの足し合わせ \begin{equation} P(r) = A r^{-n} + B r^{n} \end{equation} も解になる。これは2つの任意定数 \(A,B\) を含んでいるから微分方程式\eqref{eq4}の一般解である。ただし \(n=0\) の場合には少し注意が必要だ。\(n=0\) のときには \(r^{n}\) も \(r^{-n}\) も共に \(1\) となってしまうので、この場合は2つの独立な解の足し合わせにならない。そこで \(n=0\) の場合だけは慎重に考えることにする。\(n=0\) の場合の微分方程式\eqref{eq4}は \begin{equation} \frac{d}{dr} P'(r) = -\frac{1}{r} P'(r) \5 \Bigl( P'(r) = \frac{d}{dr} P(r) \Bigr) \end{equation} である。これは変数分離形なので簡単に積分することができて \begin{equation*} P'(r) = \frac{A}{r} \end{equation*} となる。したがって \(n=0\) の場合には \begin{equation} P(r) = A \ln r + B \end{equation} が一般解である（これは2つの任意定数 \(A,B\) を含んでいる）。まとめると \(P(r)\) は \begin{equation} P(r) = \begin{cases} A \ln r + B & ( n = 0 ) \\[5pt] A r^{-n} + B r^{n} & ( n = 1, 2, 3, \dots ) \end{cases} \label{p} \end{equation} となる。

以上、少し計算が長くなったが、もともと求めたかったものは物質内に生じた電位を表す関数であり、それは \(\phi(r,\theta)=P(r)\2Q(\theta)\) であったから、式\eqref{q}と\eqref{p}より \begin{equation} \phi(r,\theta) = \begin{cases} \ \, A \ln r + B & ( n = 0 ) \\[5pt] ( A r^{-n} + B r^{n} ) ( C \cos n \theta + D \sin n \theta ) & ( n = 1, 2, 3,\dots ) \end{cases} \end{equation} を得る。ところで、最初のラプラス方程式\eqref{laplace5}には \(n\) などという定数は現れておらず、今のところこの \(n\) はいくつであってもよい。また、\(n\) の異なる解を足し合わせたものもやはりラプラス方程式の解になっており、そのため最も一般的にはすべての \(n\) について足し合わせをした \begin{equation} \phi(r,\theta) = A_{0} \ln r + B_{0} + \sum_{n=1}^{\infty} ( A_{n} r^{-n} + B_{n} r^{n} ) ( C_{n} \cos n \theta + D_{n} \sin n \theta ) \label{phi} \end{equation} もラプラス方程式の解ということになるだろう。実はこれが偏微分方程式\eqref{laplace5}の一般解である。あとは境界条件を満足するように定数 \(A_{n},B_{n},C_{n},D_{n}\) の値を決めていけばよい。

定常電流の問題における境界条件を思い出しておこう。それは \begin{align} \nabla &\phi \cdot \bm{n} = 0 & &\text{（物質と外側の空間の境界面 \(S_{0}\) 上において）} \label{boundary10} \\[5pt] &\phi = \text{一定} & &\text{（物質と電極の境界面 \(S_{k}\) 上において）} \label{boundary11} \\[3pt] \int_{S_{k}} \nabla \phi &\cdot \bm{n} \, dS = \frac{I_{k}}{\sigma} & &\text{（\(\,k=1,2,\dots,N\,\)）} \label{boundary12} \end{align} というものであった（今考えている問題では電極の数が2つだけなので \(N=2\) である）。上で求めた一般解に対して、まずは境界条件\eqref{boundary10}を適用してみる。一般解\eqref{phi}の勾配は次のようになる： \begin{align} \nabla \phi(r,\theta) &= \Bigl( \bm{e}_{r} \frac{\d}{\d r} + \bm{e}_{\theta} \frac{1}{r} \frac{\d}{\d\theta} + \bm{e}_{z} \frac{\d}{\d z} \Bigr) \, \phi(r,\theta) \notag \\[3pt] &= \frac{\bm{e}_{r}}{r} \, \Bigl( A_{0} + \sum_{n=1}^{\infty} \, n \, ( -A_{n} r^{-n} + B_{n} r^{n} ) ( C_{n} \cos n \theta + D_{n} \sin n \theta ) \Bigr) \notag \\ & \4 + \frac{\bm{e}_{\theta}}{r} \sum_{n=1}^{\infty} \, n \, ( A_{n} r^{-n} + B_{n} r^{n} ) ( -C_{n} \sin n \theta + D_{n} \cos n \theta ) \end{align} 最初に \(\theta=0\) の境界面を考えることにすると、この面で物質の外側を向く単位法線ベクトルは \(\bm{n}=-\bm{e}_{\theta}\) であるから、ここでの境界条件は \begin{equation} \nabla \phi \cdot \bm{n} = -\frac{1}{r} \sum_{n=1}^{\infty} \, n \, ( A_{n} r^{-n} + B_{n} r^{n} ) \, D_{n} = 0 \end{equation} という式になる。この中で \(r\) についてのローラン級数が境界上、とくに \(a\le r\le b\) の範囲で \(r\) を自由に動かしても恒等的に \(0\) となるのは、\(r^{n},r^{-n}\) に掛かる係数がすべて \(0\) となるようなときだけである。そのためには \(A_{n} = B_{n} = 0\) もしくは \(D_{n} = 0\) でなければならないが（もちろん \(A_{n}=B_{n}=D_{n}=0\) であってもよいのだが）、\(A_{n}=B_{n}=0\) のほうを採用してしまうと、元の一般解へそれらを代入したときに \(C_{n},D_{n}\) の値によらず無限級数の部分が完全に消えてしまう。そのため、ひとまずはより制限のゆるい \begin{equation} D_{n} = 0 \4 ( n = 1, 2, 3, \dots ) \end{equation} という条件を採用しておいたほうが安全だろう。このとき電位 \(\phi\) の関数形は \begin{equation} \phi(r,\theta) = A_{0} \ln r + B_{0} + \sum_{n=1}^{\infty} ( A_{n} r^{-n} + B_{n} r^{n} ) \cos n \theta \label{phi2} \end{equation} という形に制限される。（ただし \(A_{n}C_{n},\,B_{n}C_{n}\) を改めて \(A_{n},B_{n}\) と置いた。\(A_{n},B_{n},C_{n}\) は今のところ任意の定数であるから \(A_{n}C_{n},B_{n}C_{n}\) という書き方は冗長である。） 同様にして左側の境界（\(\,\theta=\pi,\ \bm{n}=\bm{e}_{\theta}\,\)）も考えたいのだが、その計算はいま行った \(\theta=0\) の計算とほとんど同じであり、その結果として結局なにも新しい条件は得られないため詳細については省略する。

次に2つ目の境界条件、すなわち電極上で電位一定の条件\eqref{boundary11}を考えてみよう。まず、内側にある半径 \(a\) の電極表面上で \(\phi\) が一定となることより \begin{equation} \phi(a,\theta) = A_{0} \ln a + B_{0} + \sum_{n=1}^{\infty} ( A_{n} a^{-n} + B_{n} a^{n} ) \cos n \theta \end{equation} という式が \(0\le\theta\le\pi\) の範囲で \(\theta\) によらず一定とならなければならない。そのためには \(A_{n},B_{n}\) がどのようになっていなければならないか？ これを見るために、この式の両辺に \(\cos m\theta\ (m=1,2,3,\dots)\) を掛けて \(0\le\theta\le\pi\) の範囲で積分してみよう。三角関数の積分について \begin{equation*} \int_{0}^{\pi} \cos m \theta \, d\theta = 0, \3 \int_{0}^{\pi} \cos m \theta \cos n \theta \, d\theta = \begin{cases} \pi/2 & ( m = n ) \\ 0 & ( m \neq n ) \end{cases} \end{equation*} が成り立つこと、および \(\phi(a,\theta)\) が \(0\le\theta\le\pi\) の範囲で一定値をとることに注意すると \begin{equation*} A_{m} a^{-m} + B_{m} a^{m} = 0 \5 ( m = 1, 2, 3, \dots ) \end{equation*} という式を得る。まったく同様にして、物質の外側にある内径 \(b\) の電極上でも同じ計算を行うと、今度は \begin{equation*} A_{m} b^{-m} + B_{m} b^{m} = 0 \5 ( m = 1, 2, 3, \dots ) \end{equation*} という式が出てくる。これらは行列を使ってまとめて書くことができて \begin{equation} \begin{bmatrix} a^{-m} & a^{m} \\ b^{-m} & b^{m} \end{bmatrix} \begin{bmatrix} A_{m} \\ B_{m} \end{bmatrix} = 0 \label{matrix} \end{equation} と表せるが、今考えている問題では \(a\neq b\) なので \begin{equation*} \det \begin{bmatrix} a^{-m} & a^{m} \\ b^{-m} & b^{m} \end{bmatrix} = \Bigl( \frac{b}{a} \Bigr)^{m} - \Bigl( \frac{a}{b} \Bigr)^{m} \neq 0 \end{equation*} より、式\eqref{matrix}の \(2\times2\) 行列は逆行列を持つこととなって、それを左から掛けることで \begin{equation*} \begin{bmatrix} A_{m} \\ B_{m} \end{bmatrix} = 0 \end{equation*} を得る。すなわち \begin{equation} A_{n} = B_{n} = 0 \5 ( n = 1, 2, 3, \dots ) \end{equation} ということになる。そしてこれを式\eqref{phi2}へ代入すれば、後半の無限和の部分は完全に消えてしまって \begin{equation} \phi = A_{0} \ln r + B_{0} \label{phi3} \end{equation} という非常に簡単な式になる。

最後に、電流の条件 \begin{equation} \int_{S_{k}} \nabla \phi \cdot \bm{n} \, dS = \frac{I_{k}}{\sigma} \end{equation} を見てみよう。まず半径 \(a\) の半円形電極の表面 \(S_{1}\) 上において、そこでは物質の表面外側に立てた単位法線ベクトルが \(\bm{n}=-\bm{e}_{r}\) であり、また電極から物質に流れ出す電流は全部で \(I\) になるから \begin{equation} \int_{S_{1}} \nabla \phi \cdot ( -\bm{e}_{r} ) \, dS = \frac{I}{\sigma} \label{eq5} \end{equation} が成り立てばよい。電位\eqref{phi3}の勾配は \begin{equation*} \nabla \phi = \Bigl( \bm{e}_{r} \frac{\d}{\d r} + \bm{e}_{\theta} \frac{1}{r} \frac{\d}{\d\theta} + \bm{e}_{z} \frac{\d}{\d z} \Bigr) \, ( \ A_{0} \ln r + B_{0} ) = \frac{A_{0}}{r} \bm{e}_{r} \end{equation*} となり、また物質の厚さが \(d\) だったことを思い出すと、式\eqref{eq5}の面積分は \begin{equation*} \int_{S_{1}} \nabla \phi \cdot ( -\bm{e}_{r} ) \, dS = \int_{0}^{d} \! dz \int_{0}^{\pi} a \, d\theta \, \Bigl( \frac{A_{0}}{a} \bm{e}_{r} \Bigr) \cdot ( -\bm{e}_{r} ) = -\pi d A_{0} \end{equation*} と計算される。そしてこれが \(I/\sigma\) と等しいことより、定数 \(A_{0}\) は \begin{equation} A_{0} = -\frac{I}{\pi d\sigma} \end{equation} となる。同じ計算を外側にある内径 \(b\) の電極表面（物質へ流れ出す電流 \(-I\)、物質の表面外側に立てた単位法線ベクトル \(\bm{n}=\bm{e}_{r}\) ）に対しても行うことになるが、今やったのとまったく同じ結果となり、何も新しい条件は出てこないため省略する。

以上をまとめると電位 \(\phi\) の関数形が \begin{equation} \phi = -\frac{I}{\pi d\sigma} \, \ln r + B_{0} \end{equation} と求まったことになる。定数 \(B_{0}\) は電位の基準の取り方の任意性から生じた定数でありユニークには決まらない。しかしながら、例えば、物質の外側にある陰極の表面（\(\,r=b\,\)）における電位を \(0\) と定義することにすると \begin{equation*} \phi(b) = -\frac{I}{\pi d\sigma} \, \ln b + B_{0} = 0 \end{equation*} より \begin{equation} B_{0} = \frac{I}{\pi d\sigma} \, \ln b \end{equation} と決まるので \begin{equation} \phi = \frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{b}{r} \Bigr) \4 ( a \le r \le b ) \label{phi4} \end{equation} とすることができる。最後に、物質内を流れる電流密度はオームの法則 \(\bm{i}=-\sigma\2\nabla\phi\) によって \begin{equation} \bm{i} = \frac{I}{\pi d} \frac{\bm{e}_{r}}{r} \4 ( a \le r \le b ) \end{equation} と求められる。電流は陽極から陰極へ向かって放射状に広がっていくことがわかる。

重ね合わせの原理の具体例

重ね合わせの原理を使ってもう1つ定常電流の問題を解いてみよう。

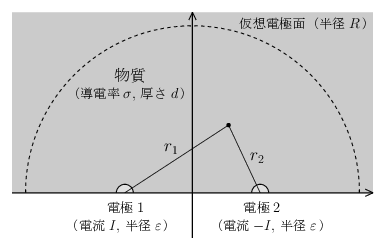
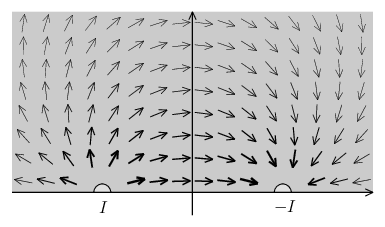
上半平面全体に半無限的に広がった一様なシート状物質（導電率 \(\sigma\)、厚さ \(d\,\)）に発生する電位の分布と電流密度を求めたい。この物質には \(x\) 軸上の2か所に小さな半円形の金属電極（半径 \(\varepsilon\)、厚さ \(d\,\)）が取り付けられおり、電極1から電極2のほうに向けて大きさ \(I\) の電流が流れている。

この問題を直接解くこともできるのかもしれないが、ここでは上の例題で求めた結果と重ね合わせの原理を使って問題を解いてみる。電極1と電極2の中点を中心とする、大きな半径 \(R\) をもった仮想的な導体電極（電極3）を考えよう（上図破線の半円、\(z\) 軸方向の高さは \(d\,\)）。今知りたいのは電極1から電極2に向けて電流 \(I\) を流したときに生じる電位 \begin{equation} \phi = \varPhi(\bm{r},\,I,-I,0) \end{equation} であるが、これを電極1から電極3へ電流 \(I\) を流したときに発生する電位 \(\phi_{1}=\varPhi(\bm{r},\,I,0,-I)\) と、電極3から電極2へ電流 \(I\) を流したときに発生する電位 \(\phi_{2}=\varPhi(\bm{r},\,0,-I,I)\) の2つに分けてしまう。すなわち \begin{equation} \phi = \phi_{1} + \phi_{2} \end{equation} \begin{equation} \varPhi(\bm{r},\,I,-I,0) = \varPhi(\bm{r},\,I,0,-I) + \varPhi(\bm{r},\,0,-I,I) \end{equation} と分解する。（電極3は実際には存在しない仮想的な導体電極であるが、そこへ流れ込む電流とそこから流れ出す電流の量が同じで、正味の電流は \(0\) だから問題ないだろう。また、この仮想電極が存在する場所は \(R\to\infty\) の極限で無限遠点（半無限物質の境界）となる。） このとき、電極1から電極3へ電流を流している状況が、前の節で見た半円形物質に対する問題設定と非常によく似ていることに気づくだろうか。異なる点というと、電極1と電極3でそれぞれの中心点が一致していないことであるが、これは \(R\to\infty\) の極限では一致してると考えてよさそうである。また電位 \(\phi_{1}\) に対しては、電極2の表面においても電位一定の境界条件が課されることになるのだが、これも \(\varepsilon\to0\) の極限では無視してよいだろう（より正確には、電極1と電極2の間の距離に比べて \(\varepsilon\) が十分に小さい場合に無視できる）。したがって、前節の半円形物質で求めた電位の式\eqref{phi4}は、今の問題における \(\phi_{1}\) の近似解としてそのまま用いることができる： \begin{equation} \phi_{1} = \frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{R}{r_{1}} \Bigr) \end{equation} ただし \(r_{1}\) は、電極1の中心から測った物質内の任意の点までの距離である。電極3から電極2へ電流を流したときに発生する電位 \(\phi_{2}\) を求める方法も同じである。\(\phi_{1}\) と異なる点は、電流の符号が反転していること、および電極2の中心の位置が変わっていることだけである。そのため \begin{equation} \phi_{2} = -\frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{R}{r_{2}} \Bigr) \end{equation} が近似解となる（\(\,r_{2}\) は電極2の中心から測った距離）。あとは \(\phi_{1}\) と \(\phi_{2}\) を重ね合わせれば本来の電位 \(\phi\) が求まることになる： \begin{equation} \phi = \phi_{1} + \phi_{2} = \frac{I}{\pi d\sigma} \, \ln \Bigl( \frac{r_{2}}{r_{1}} \Bigr) \end{equation} ただし電位 \(0\) の基準点は無限遠点にとっている。この式は \(\varepsilon\to0\) の極限でこの問題の厳密解となる。

最後に物質内に現れる電流密度の分布を求めよう。それにはオームの法則 \begin{equation} \bm{i} = -\sigma \2 \nabla \phi \label{ohm4} \end{equation} を用いればよいのだが、今求めた電位の表式は原点の異なる2つの円柱座標系 \((r_{1},\theta_{1},z),\,(r_{2},\theta_{2},z)\) を使って書かれているため計算が少し面倒くさそうに見える。しかしながら、対数の性質によって \(r_{1}\) と \(r_{2}\) は分離できるので、それらに対して別々の表現でナブラ演算子を作用させれば式\eqref{ohm4}の微分演算は簡単に実行できる。すなわち \begin{equation} \nabla = \Bigl( \bm{e}_{r_{1}} \frac{\d}{\d r_{1}} + \bm{e}_{\theta_{1}} \frac{1}{r_{1}} \frac{\d}{\d\theta_{1}} + \bm{e}_{z} \frac{\d}{\d z} \Bigr) = \Bigl( \bm{e}_{r_{2}} \frac{\d}{\d r_{2}} + \bm{e}_{\theta_{2}} \frac{1}{r_{2}} \frac{\d}{\d\theta_{2}} + \bm{e}_{z} \frac{\d}{\d z} \Bigr) \end{equation} という2つの表現をうまく使い分けて \begin{align} \bm{i} &= -\sigma \2 \nabla \phi \notag \\[3pt] &= -\frac{I}{\pi d} ( \nabla \ln r_{2} - \nabla \ln r_{1} ) \notag \\[5pt] &= \frac{I}{\pi d} \Bigl( \frac{\bm{e}_{r_{1}}}{r_{1}} - \frac{\bm{e}_{r_{2}}}{r_{2}} \Bigr) \end{align} を得る。