単位長さあたりの巻き数が \(n\) の無限に長いソレノイドコイルがつくる磁場を求めてみよう。コイルには大きさ \(I\) の電流が流れている。
電磁気学の問題を解く上で基本となるのはマクスウェル方程式 \begin{align} &\nabla \cdot B = 0, & &\nabla \op H = i + \frac{\d D}{\d t} \\[3pt] &\nabla \cdot D = \rho, & &\nabla \op E = -\frac{\d B}{\d t} \end{align} である。とくに、静磁場(時間的に変動しない磁場)の問題を考える上で必要となるのは、磁場に関するガウスの法則 \begin{equation} \nabla \cdot B = 0 \label{gauss} \end{equation} とアンペールの法則 \begin{equation} \nabla \op H = i \label{ampere0} \end{equation} の2つだけになる。ただし、\(B\) は磁束密度、\(H\) は磁場の強さ、\(i\) は電流密度を表す。空気の透磁率を \(\mu\) とすると(これは真空の透磁率 \(\mu_{0}\) にほぼ等しい)、磁場の強さと磁束密度のあいだには \begin{equation} B = \mu H \end{equation} の関係があるので、以下では空気中を想定し、\(B\) だけを使って式を書いていくことにしよう。このとき、アンペールの法則\eqref{ampere0}は \begin{equation} \nabla \op B = \mu \1 i \label{ampere} \end{equation} と書かれることになる。
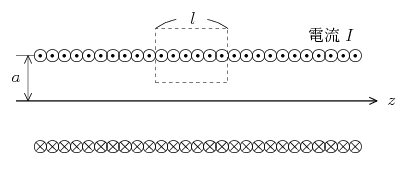
まず最初にやるべきことは座標系を設定することである。ソレノイドは(長さ無限大の)円柱形であるから、この問題では円柱座標 \((r,\theta,z)\) を用いるのが便利だろう。そこでソレノイドの中心軸にそって \(z\) 軸をとることにして、電線を流れる電流の向きと一致するように \(\theta\) 方向を定める。\(z\) 軸の正の向きは、\(r,\theta,z\) 方向の各単位ベクトル \(e_{r},\,e_{\theta},\,e_{z}\) がこの順で右手系をなすように決めるものとする。このように座標系を定めると、電流密度ベクトル \(i\) は、ディラックのデルタ関数を使って \begin{equation} i = n I \1 \delta(r-a) \, e_{\theta} \label{current} \end{equation} と表すことができる。ただし、\(n\) はソレノイドコイルの単位長さあたりの巻き数、\(I\) は電線を流れる電流の大きさ、\(a\) はソレノイドの半径、\(e_{\theta}\) は \(\theta\) 方向の単位ベクトルである。なお、ディラックのデルタ関数とは \begin{equation} \int_{r_{1}}^{r_{2}} \delta(r-a) \, dr = \begin{cases} \, 1 \ & \text{積分区間 \([\2r_{1},\,r_{2}\2]\) が \(a\) を含む場合} \\[3pt] \, 0 \ & \text{積分区間 \([\2r_{1},\,r_{2}\2]\) が \(a\) を含まない場合} \end{cases} \label{delta} \end{equation} となる性質をもつ。式\eqref{current}が正しいことは、上の図の破線で示した長方形領域(横幅 \(l\) で \(e_{\theta}\) に直交する)において電流密度ベクトル \(i\) を面積分したときに、その面を貫く全電流 \(nI\1l\) が正しく得られることから理解できると思う。
さて、座標系が定まったのでさっそく微分方程式を解いていきたいが、微分方程式を持ち出さずとも、磁場 \(B=(B_{r},B_{\theta},B_{z})\) に対しては系の対称性だけからある程度の制限がついてしまう。というのも、無限に長いソレノイドコイルでは \(z\) 軸方向の並進対称性(すなわち \(z\) 軸方向へ平行移動しても系の様子が移動前と何も変わらない)があるため、磁場が \(z\) 座標に依存することはありえない(もしこれが \(z\) 座標に依存して変化したとすると、\(z\) 座標に関してはどこも対等であるはずの世界で、磁場が特別に大きい点や小さい点が出てきてしまう)。同様の理屈で、\(\theta\) 軸方向の移動(回転)によっても系の様子は何も変化しないから、磁場が \(\theta\) に依存することもない。したがって、磁場 \(B\) は動径 \(r\) だけの関数であり \begin{equation} B = ( \, B_{r}(r), \, B_{\theta}(r), \, B_{z}(r) \, ) \end{equation} という形をしていなければならない。(円柱座標で見た磁場は \(\theta\) に依存しないのであるが、通常の \(xyz\)-座標系から見たときには偏角 \(\theta\) の値に応じて \(r\) 方向や \(\theta\) 方向が変化することには注意しよう。\(xyz\)-座標から見ると、\(\theta\) 方向の回転によって \(B_{r}\) や \(B_{\theta}\) の向きが \(\theta\) の関数として規則的に変化(回転)する。)
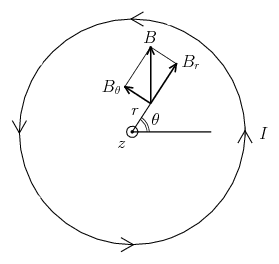
それでは実際に微分方程式\eqref{gauss}、\eqref{ampere}を解いて磁場 \(B\) の3つの成分を計算していこう。ベクトル解析の公式によると、円柱座標系におけるベクトル場の発散や回転は次で与えられる(\(\,A\) は任意のベクトル場): \begin{equation} \nabla \cdot A = \frac{1}{r} \frac{\d}{\d r} (rA_{r}) + \frac{1}{r} \frac{\d A_{\theta}}{\d\theta} + \frac{\d A_{z}}{\d z} \end{equation} \begin{equation} \nabla \op A = \Bigl( \frac{1}{r} \frac{\d A_{z}}{\d\theta} - \frac{\d A_{\theta}}{\d z} \Bigr) \, e_{r} + \Bigl( \frac{\d A_{r}}{\d z} - \frac{\d A_{z}}{\d r} \Bigr) \, e_{\theta} + \Bigl( \frac{1}{r} \frac{\d}{\d r} (rA_{\theta}) - \frac{1}{r} \frac{\d A_{r}}{\d\theta} \Bigr) \, e_{z} \end{equation} これらを使って式\eqref{gauss}と\eqref{ampere}を円柱座標の成分で表してみたい。磁場が \(\theta\) や \(z\) に依存しないこと、および式\eqref{current}の電流密度の表式を代入すると \begin{equation} \nabla \cdot B = \frac{1}{r} \frac{d}{dr} (rB_{r}) = 0 \end{equation} \begin{equation} \nabla \op B = -\frac{dB_{z}}{dr} \, e_{\theta} + \frac{1}{r} \frac{d}{dr} (rB_{\theta}) \, e_{z} = \mu n I \delta(r-a) \, e_{\theta} \end{equation} すなわち \begin{equation} \frac{d}{dr} (rB_{r}) = 0 \label{eq1} \end{equation} \begin{equation} \frac{d}{dr} (rB_{\theta}) = 0 \label{eq2} \end{equation} \begin{equation} \frac{dB_{z}}{dr} = -\mu n I \1 \delta(r-a) \label{eq3} \end{equation} という3つの常微分方程式が得られる。3つの未知関数 \(B_{r}(r),\,B_{\theta}(r),\,B_{z}(r)\) に対して微分方程式も3つであるから丁度いい。まず、動径成分 \(B_{r}\) に対する微分方程式は簡単に解ける: \begin{equation} r \1 B_{r} = C \ \ \text{(定数)} \end{equation} より \begin{equation} B_{r}(r) = \frac{C}{r} \end{equation} となる。任意定数 \(C\) の値は境界条件から決定する。動径 \(r\) の定義域は \([\2 0,\infty)\) であるので、その境界は \(0\) と \(\infty\) になるが、とくに原点 \(r=0\) において磁場が有限でなければならないことより \(C=0\) が要請される。つまり \begin{equation} B_{r}(r) = 0 \end{equation} である。次に偏角成分 \(B_{\theta}\) を考えると、微分方程式\eqref{eq2}の形は式\eqref{eq1}と全く同じであるから、動径成分と同様の計算によって \begin{equation} B_{\theta}(r) = 0 \end{equation} が結論される。
最後に式\eqref{eq3}の \(z\) 方向成分に関する微分方程式 \begin{equation} \frac{dB_{z}}{dr} = -\mu n I \1 \delta(r-a) \label{eq4} \end{equation} を解こう。このようなデルタ関数を含む微分方程式が現れた場合の定石であるが、デルタ関数が発散する点を境界にして元の微分方程式を2つの領域に分割し、それぞれの領域で微分方程式を独立に解いた上で、最後にそれら2つの解をうまく接続する。今の問題で \(\delta(r-a)\) が発散する点は \(r=a\) であるので、この点を境界として2つの微分方程式 \begin{align} &\frac{dB_{z}}{dr} = 0 \4 ( r \lt a ) \\[5pt] &\frac{dB_{z}}{dr} = 0 \4 ( r \gt a ) \end{align} に分ける(デルタ関数 \(\delta(r-a)\) は \(r=a\) という1点を除けば常に \(0\) である)。これらの微分方程式は簡単に解くことができて \begin{equation} B_{z}(r) = \begin{cases} C_{\mr{in}} \ \ & ( r \lt a ) \\[3pt] C_{\mr{ex}} \ \ & ( r \gt a ) \end{cases} \label{bz} \end{equation} となる。ここで \(C_{\mr{in}},\,C_{\mr{ex}}\) は単なる積分定数であるが、両者が同じ値をとる必要はないことに注意しよう。ただ、1階微分方程式に現れる任意定数の数は1つだけになるはずなので、これら \(C_{\mr{in}}\) と \(C_{\mr{ex}}\) の間には何らかの関係性がある。その関係を見るために、ソレノイド内部の任意の動径を \(r_{\mr{in}}\)、ソレノイド外部の任意の動径を \(r_{\mr{ex}}\) として、区間 \([\2r_{\mr{in}},\,r_{\mr{ex}}\2]\) で微分方程式\eqref{eq4}の両辺を定積分してみる: \begin{equation} \int_{r_{\mr{in}}}^{r_{\mr{ex}}} \frac{dB_{z}}{dr} \, dr = -\mu n I \int_{r_{\mr{in}}}^{r_{\mr{ex}}} \delta(r-a) \, dr \end{equation} この右辺にデルタ関数の性質\eqref{delta}を使えば \begin{equation} B_{z}(r_{\mr{ex}}) - B_{z}(r_{\mr{in}}) = -\mu n I \end{equation} となるので、\(r_{\mr{in}}\lt a\lt r_{\mr{ex}}\) に注意して式\eqref{bz}を代入すれば \begin{equation} C_{\mr{in}} = \mu n I + C_{\mr{ex}} \end{equation} という関係を得る。そしてこれより、磁場の \(z\) 方向成分の一般解 \begin{equation} B_{z}(r) = \begin{cases} \mu n I + C_{\mr{ex}} & ( r \lt a ) \\[3pt] C_{\mr{ex}} & ( r \gt a ) \end{cases} \end{equation} が求まる。\(C_{\mr{ex}}\) は微分方程式だけからは決めることのできない真の任意定数で、境界条件を課すことでその値を決定する。「無限長のソレノイド」という現実には存在しない系であるため、これに適当な境界条件を与えることは少し難しいが、「十分に長いソレノイドコイルの中央付近の磁場は \(\mu nI\) に漸近する」という実験事実より、ソレノイド内部の磁場が \(B_{z}(r)=\mu nI\) になるように \begin{equation} C_{\mr{ex}} = 0 \end{equation} と取るのが現実的な境界条件であろう。
以上をまとめると、無限に長いソレノイドコイルがつくる磁場は \begin{equation} B = \begin{cases} \mu n I \1 e_{z} & \text{ソレノイド内部} \\[3pt] \ 0 & \text{ソレノイド外部} \end{cases} \end{equation} となる。ソレノイドの内部であれば、電線に近いところも離れたところも、どこでも同じ磁場 \(\mu nI\1e_{z}\) が発生しているというのは少し意外な結果かもしれない。また、無限長のソレノイドには端が存在しないため、内部の磁束の漏れ出しはなく、ソレノイド外部では至るところで磁場が \(0\) となる。現実には無限に長いソレノイドコイルを用意することなどできないのであるが、その半径に対して十分に長い軸長を持つソレノイドを用意することができれば、その内部の中央付近では近似的に一様と見なせる磁場を発生させることができる。