ガウス分布の導出

偶然誤差の性質から確率論や統計学でよく用いられるガウス分布（正規分布）を導出してみよう。

真の値 \(X\) をもつある量の測定を行うことを考える。この測定には系統誤差は含まれず、偶然誤差のみが発生するものとしよう。偶然誤差については経験にもとづく次のガウスの公理がある：

大きさの等しい正と負の誤差は等しい確率で生じる。
小さい誤差は大きい誤差より起こりやすい。
ある限界値より大きな誤差は実際上起こらない。

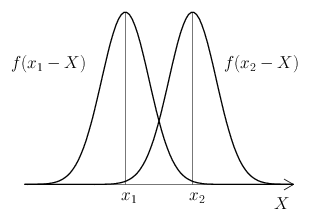
さて、具体的にある測定を実施することで得られた測定値を \(x\) とすると、そのときの誤差 \(\varepsilon\) は \begin{equation} \varepsilon = x - X \label{error} \end{equation} で与えられる。ある大きさの偶然誤差が発生する確率を誤差 \(\varepsilon\) の関数とし、その確率密度関数を \(f(\varepsilon)\) と置くことにすれば、確率密度関数の性質より、誤差の大きさが \(\varepsilon\) と \(\varepsilon+d\varepsilon\) の間に入る確率は \begin{equation*} f(\varepsilon) \, d\varepsilon \end{equation*} である。式\eqref{error}より \(d\varepsilon=dx\) であるから、これを \begin{equation*} f(x-X) \, dx \end{equation*} と表してもよい。確率密度関数 \(f\) の関数形を求めることがこのページの目的となる。

同一の条件で \(n\) 回の測定を行うことを考える。このとき \(n\) 個の測定値は偶然誤差によって様々にバラつくこととなるが、それらが \(x_{1},x_{2},\dots,x_{n}\) という値から \(dx\) 以内の範囲に入る確率は \begin{equation*} f(x_{1}-X) \, dx \ f(x_{2}-X) \, dx \dotsm f(x_{n}-X) \, dx \end{equation*} で与えられる。この確率を \(P\,dx^{n}\) と置くことにすると、確率密度 \(P\) は \begin{equation} P = f(x_{1}-X) \, f(x_{2}-X) \dotsm f(x_{n}-X) \label{p} \end{equation} である。\(x_{1},x_{2},\dots,x_{n}\) を確率変数と見たとき、これを同時確率密度関数という。この関数は、\(n\) 回の測定の測定結果として \(x_{1},x_{2},\dots,x_{n}\) という測定値が得られる確率の確率密度を与えるものであるが、このような見方をした場合、ふつう真の値 \(X\) には何か既知の値が与えられていることを想定する。ところが現実の測定においては話が逆で、我々が知ることができるのは測定値 \(x_{1},x_{2},\dots,x_{n}\) の方である。真の値 \(X\) はふつう未知であり、それを求めるために測定を行うのである。そして我々はできるだけ偶然誤差の影響を減らそうとして、1回だけではなく複数回の測定を行い、複数の測定値の相加平均 \begin{equation} \bar{x} = \frac{x_{1}+x_{2}+\dots+x_{n}}{n} \label{mean} \end{equation} によって真の値 \(X\) を推定する。

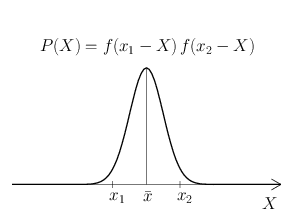
さて、ガウスの公理の最初の2つより、\(f(x-X)\) は \(\varepsilon=0\) すなわち \(x=X\) において最大値をとるから、その積で与えられる同時確率密度関数 \(f(x_{1}-X)\,f(x_{2}-X)\dotsm f(x_{n}-X)\) も明らかに \(x_{1}=x_{2}=\dots=x_{n}=X\) で最大値をとる。では逆に、\(x_{1},x_{2},\dots,x_{n}\) が既知の値として与えられているときに、\(X\) を独立変数と見た場合の式\eqref{p}右辺の関数 \begin{equation} P(X) = f(x_{1}-X) \, f(x_{2}-X) \dotsm f(x_{n}-X) \label{px} \end{equation} はどのような \(X\) において最大値をとるだろう？実はこの答えは自明ではない。しかしながら、\(P\) は真の値において最大値をとる量であることと、偶然誤差に対しては式\eqref{mean}の \(\bar{x}\) から真の値を推定できるという経験則から次を仮定することにしよう： \begin{equation} P(X) \ \, \text{は} \ \, X=\bar{x} \ \, \text{で最大値をとる。} \label{postulate} \end{equation} すなわち \(P'(\bar{x})=0\) を仮定する。

以上で \(f\) の関数形を求める準備が整った。まず式\eqref{px}の両辺の自然対数をとる： \begin{equation*} \ln P(X) = \sum_{i=1}^{n} \, \ln f(x_{i}-X) \end{equation*} そしてこれを \(X\) で微分してみよう： \begin{equation*} \frac{P'(X)}{P(X)} = -\sum_{i=1}^{n} \frac{f'(x_{i}-X)}{f(x_{i}-X)} \end{equation*} ここで \(X\) に \(\bar{x}\) を代入すると \(P'(\bar{x})=0\) より \begin{equation} \sum_{i=1}^{n} \frac{f'(x_{i}-\bar{x})}{f(x_{i}-\bar{x})} = 0 \label{eq1} \end{equation} がわかる。また、式\eqref{mean}を少し変形すると \begin{equation} \sum_{i=1}^{n} \, ( x_{i} - \bar{x} ) = 0 \label{eq2} \end{equation} という関係式を得る。ここで次の補題を証明する。

補題　\(\phi(\cdot)\) をすべての実数で定義された微分可能な関数とする。\(n\) を \(3\) 以上の整数として、\(n\) 個の変数 \(x_{1},x_{2},\dots,x_{n}\) が \begin{equation} \sum_{i=1}^{n} \, x_{i} = 0 \label{x} \end{equation} を満足するように動くとき、常に \begin{equation} \sum_{i=1}^{n} \, \phi(x_{i}) = 0 \label{phi} \end{equation} という関係式が成立しているならば、\(\phi\) の関数形は \(a\) を任意の定数として \(\phi(x)=ax\) である。

証明　変数は \(n\) 個あるが束縛条件\eqref{x}によって、独立に動かすことのできる変数は \(n-1\) 個である。そこで最後の変数 \(x_{n}\) を \begin{equation} x_{n} = -\sum_{i=1}^{n-1} \, x_{i} \label{xn} \end{equation} によって消去し、\(x_{1},\dots,x_{n-1}\) を独立に動かすことのできる変数と見る。このとき、式\eqref{phi}の両辺を \(x_{1}\) で偏微分すると \begin{equation*} \phi'(x_{1}) + \phi'(x_{n}) \frac{\d x_{n}}{\d x_{1}}= 0 \end{equation*} になるが、式\eqref{xn}より \(\d x_{n}/\d x_{1}=-1\) であるから \begin{equation*} \phi'(x_{1}) = \phi'(x_{n}) \end{equation*} を得る。同様にして、式\eqref{phi}の両辺を \(x_{2}\) で偏微分すると \begin{equation*} \phi'(x_{2}) = \phi'(x_{n}) \end{equation*} となるので、前の式とあわせて \begin{equation*} \phi'(x_{1}) = \phi'(x_{2}) \end{equation*} が言える。ところで \(x_{1}\) と \(x_{2}\) はまったく独立に動かすことのできる変数であったから、この等式が成り立つためには \(\phi'(x)\) が \(x\) によらずいつも同じ値をとらなければならない。すなわち \begin{equation*} \phi'(x) = \text{定数} \end{equation*} である。これより \(a,b\) を任意の定数として \begin{equation*} \phi(x) = ax + b \end{equation*} となる。最後にこの \(\phi\) を式\eqref{phi}へ代入し、そこに\eqref{x}を使えば \(b=0\) であるとわかるので、\(\phi(x)=ax\) を得る。\(\blacksquare\)

式\eqref{eq1}と\eqref{eq2}において \((f'/f)\to\phi,\ (x_{i}-\bar{x})\to x_{i}\) という置き換えを行えば、これは補題と同じ形になる。（補題とは違って今考えている問題では \(n=2\) となる可能性もあるが、このとき上の補題は「\(\,\phi\) の関数形は任意の微分可能な奇関数」という結果に変わる。\(\phi(x)=ax\) は奇関数だから、この形は \(n=2\) の場合を加味しても有効である。なお \(n=1\) の場合は、ガウスの公理によって最初から \(P(X)=f(x_{1}-X)\) が \(X=x_{1}=\bar{x}\) で最大値をとっており、仮定\eqref{postulate}は何ら特別な条件を述べていないので、\(n=1\) の可能性は考慮しなくてよい。）よって、補題を用いれば、確率密度関数 \(f\) は \begin{equation*} \frac{f'(x)}{f(x)} = ax \end{equation*} という条件を満足していなければならず、これを積分して \begin{equation*} f(x) = C \exp \Bigl( \frac{ax^{2}}{2\:} \! \Bigl) \5 C: \text{積分定数} \end{equation*} を得る。さて、ガウスの公理の3つ目より \(\displaystyle\lim_{x\to\pm\infty}f(x)=0\) でなければならないから \(a\lt0\) がわかる。そこで、以下では \(a=-1/\sigma^{2}\) と置くことにする： \begin{equation*} f(x) = C \exp \Bigl( -\frac{x^{2}}{2\sigma^{2}} \Bigr) \end{equation*} それでは最後に、全確率が \(1\) となるように定数 \(C\) の値を定めよう。\(f(x)\) をすべての \(x\) で積分すると \begin{equation*} \int_{-\infty}^{\infty} f(x) \, dx = \int_{-\infty}^{\infty} C \exp \Bigl( -\frac{x^{2}}{2\sigma^{2}} \Bigr) \, dx = C \sqrt{2\pi\sigma^{2}} \end{equation*} となるから、これが \(1\) となるには \begin{equation*} C = \frac{1}{\sqrt{2\pi\sigma^{2}}} \end{equation*} であればよい。ただし、ガウス積分の公式 \begin{equation*} \int_{-\infty}^{\infty} e^{-kx^{2}} \, dx = \sqrt{\frac{\pi}{k}} \5 ( k \gt 0 ) \end{equation*} を使った。変数を本来の記号 \(\varepsilon\) に戻せば、最終的に偶然誤差の確率密度関数として \begin{equation*} f(\varepsilon) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \, \exp \Bigl( -\frac{\varepsilon^{2}}{2\sigma^{2}} \Bigr) \end{equation*} が得られる。あるいは、測定値に相当する変数 \(x\) を使って表せば \begin{equation*} f(x-X) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \, \exp \biggl( -\frac{(x-X)^{2}}{2\sigma^{2}} \biggr) \end{equation*} である。

以上の導出からわかるように、ガウス分布とはガウスの公理を満たす確率密度関数のうち、とくに \(P'(\bar{x})=0\) の条件を満足するものである。