不連続な関数をフーリエ級数表示し、グラフを書くとギブス現象とよばれる現象が起こる。その様子を矩形波で見てみよう。
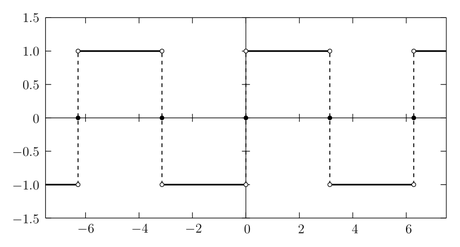
ギブス現象
\(m=0,\pm1,\pm2,\dots\) として矩形波 \begin{equation} f(x) = \begin{cases} \3 1 & \: \, 2m \pi \lt x \lt (2m+1) \pi \\[3pt] -1 \3 &(2m+1) \pi \lt x \lt (2m+2) \pi \\[3pt] \3 0 & \: \, x = 2m \pi \end{cases} \label{square} \end{equation} のフーリエ級数表示を考えよう。(不連続点 \(x=2m\pi\) における \(f(x)\) の値は \(1\) でも \(-1\) でもなんでもよいのだけれど、不連続点においてはフーリエ級数が \(f(x)\) の左右からの極限の平均値に収束するという性質に合わせて \((1+(-1))/2=0\) を選ぶことにする。) \(f(x)\) は周期 \(2\pi\) の周期関数で \begin{equation*} f(x) = \frac{a_{0}}{2} + \sum_{n=1}^{\infty} \, \bigl( \, a_{n} \cos nx + b_{n} \sin nx \, \bigr) \end{equation*} という形にフーリエ級数展開することができる。そして、そのフーリエ係数 \(a_{n},b_{n}\) は三角関数の直交性から \begin{equation*} a_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos nx \, dx \end{equation*} \begin{equation*} b_{n} = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin nx \, dx \end{equation*} と計算することができる。\(f(x)\) は奇関数だから \(a_{n}\) はすべて \(0\) となり、また \(b_{n}\) は \begin{equation*} b_{n} = \frac{2}{\pi} \int_{0}^{\pi} \sin nx \, dx = \frac{2}{\pi n} \Bigl[ -\cos nx \Bigr]_{0}^{\pi} = \begin{cases} \displaystyle \frac{4}{\pi n} \3 & n: \text{奇数} \\[5pt] \ \ 0 & n: \text{偶数} \end{cases} \end{equation*} となる。したがって \(f(x)\) のフーリエ級数表示は \begin{equation} \begin{split} f(x) &= \frac{4}{\pi} \sum_{n=0}^{\infty} \frac{\sin(2n+1)x}{2n+1} \\[3pt] &= \frac{4}{\pi} \Bigl( \sin x + \frac{1}{3} \sin 3x + \frac{1}{5} \sin 5x + \dotsb \Bigr) \end{split} \label{fourier} \end{equation} で与えられる。
式\eqref{fourier}の右辺は \(\sin\) の無限和の形で表されているが、実際にこれを計算するためには有限の \(n\) で和を打ち切らねばならない。(例えば正弦波電圧の重ね合わせによって矩形波電圧を生成することを考えると、周波数無限大の正弦波を作ることなんてできないから \(\sin\) の有限和によって矩形波を近似しなければならない。) そこで式\eqref{fourier}の部分和 \begin{equation} f_{N}(x) = \frac{4}{\pi} \sum_{n=0}^{N} \frac{\sin(2n+1)x}{2n+1} \label{sum} \end{equation} を考え、そのグラフの形がどのように矩形波へ近づいていくか見てみよう。まず \(N\) が小さいときには次のようなグラフが書ける。
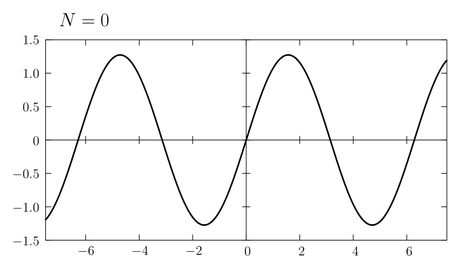
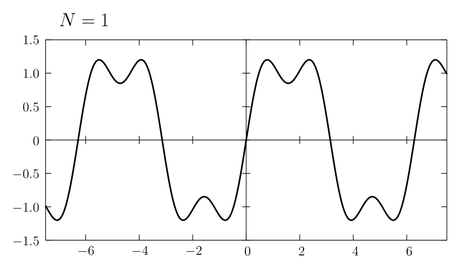
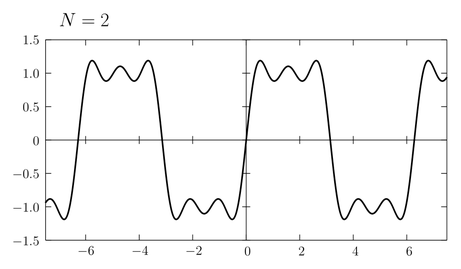
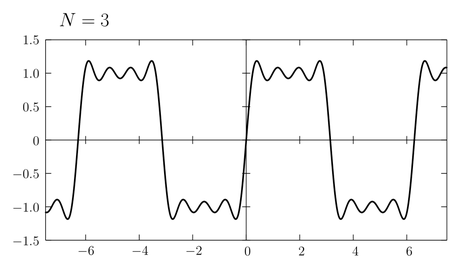
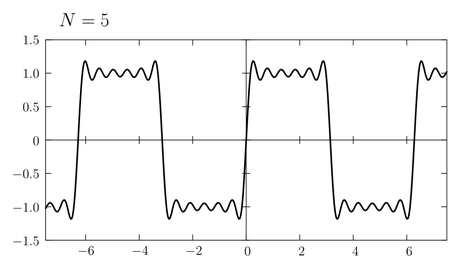
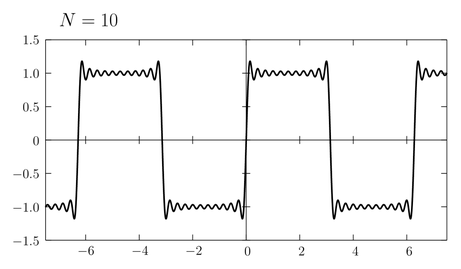
\(N\) が増加するにしたがい矩形波に近づいていくことがわかる。また \(N\) が1つ増えると半周期に1つ山や谷の数が増える。近似の精度を高めるために \(N\) をどんどん大きくしていこう。
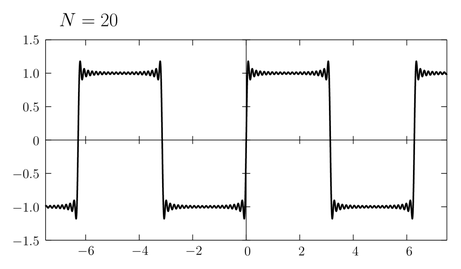
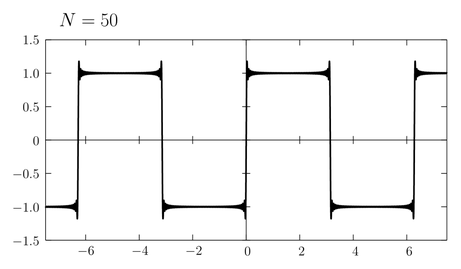
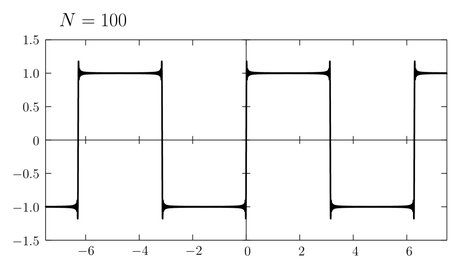
かなり矩形波に近づいてきたが不連続点近くにある「ひげ」はなかなか消えてくれない。実はこの「ひげ」は有限の \(N\) を考える限り決して消えないことが知られている。
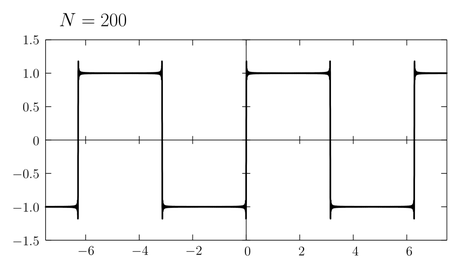
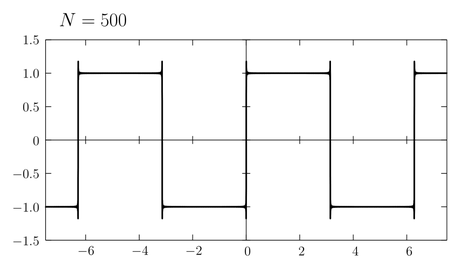
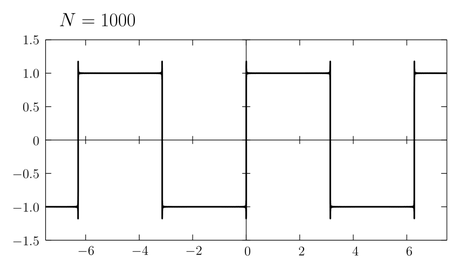
もとの関数の不連続点近傍でグラフにひげが生えるこの現象は「ギブス現象」と呼ばれている(ギブスの名は熱力学の「ギブスの自由エネルギー」で知っている人が多いと思う)。そもそも不連続関数を \(\sin\) や \(\cos\) という連続関数だけで近似しようとするのが無理な話であって、無理に近似しようとした結果このようなずれが発生したのだと考えられる。ただし \(N\to\infty\) の極限では、部分和\eqref{sum}はもとの矩形波\eqref{square}へ正確に一致する: \begin{equation} \lim_{N\to\infty} f_{N}(x) = f(x) \label{lim} \end{equation} \(N\) がどんなに大きくてもそれが有限である限り \(f_{N}(x)\) は常に連続関数であるが、その極限をとった先は不連続な関数になるのである。「極限をとる」という操作によって元の性質をはみ出すことがあることに注意しよう。連続関数の列の極限が連続関数であるとは限らない。微分可能な関数の列の極限が微分可能であるとは限らない。極限をとることによって至るところ微分不可能な関数になったり、至るところ不連続な関数ができてしまうことだってある…
関数列の一様収束
式\eqref{lim}のようにフーリエ級数の部分和 \(f_{N}(x)\) は確かに矩形波 \(f(x)\) へ収束しているのだが、それは一様収束(または広義一様収束)という性質のよい収束ではない。ここでは関数列の収束について簡単に述べることにしよう。
無限数列 \(\{a_{n}\}=a_{1},a_{2},a_{3},\dots\) がある一定の有限値 \(a\) に収束するとは、正の実数 \(\varepsilon\gt0\)(これはいくらでも小さくてよい)を任意に取ってきたとき、その \(\varepsilon\) の値によって決まる適当な自然数 \(N\) をうまく選べば、\(n\ge N\) なるすべての自然数 \(n\) に対して \(|a_{n}-a|\lt\varepsilon\) とできることである。
この文章の意味を理解するために次のような具体例を考えてみよう。数列 \(\{a_{n}\}\) の第 \(n\) 項が \begin{equation} a_{n} = \sum_{k=0}^{n} \frac{1}{k!} = 1 + \frac{1}{1!} + \frac{1}{2!} + \dots + \frac{1}{n!} \label{sequence} \end{equation} で与えられる無限数列を考えよう。この数列は \(n\to\infty\) のとき、指数関数 \(e^{x}\) のテイラー展開 \begin{equation*} e^{x} = \sum_{k=0}^{\infty} \frac{x^{k}}{k!} \end{equation*} において \(x=1\) と置いたものに一致するから \begin{equation*} \lim_{n\to\infty} a_{n} = e = 2.718281828\dots \end{equation*} に収束するはずである。実際、式\eqref{sequence}の和を具体的に計算すると \begin{align*} a_{1} \ &= 2 & a_{2} \ &= 2.5 \\ a_{3} \ &= 2.666666666\dots & a_{4} \ &= 2.708333333\dots \\ a_{5} \ &= 2.716666666\dots & a_{6} \ &= 2.718055555\dots \\ a_{7} \ &= 2.718253968\dots & a_{8} \ &= 2.718278769\dots \\ a_{9} \ &= 2.718281525\dots & a_{10} &= 2.718281801\dots \\ a_{11} &= 2.718281826\dots & a_{12} &= 2.718281828\dots \end{align*} などが得られる。まず最初に、収束の定義の \(\varepsilon\) として \(\varepsilon=1\) を選んだ場合を考えてみよう。このとき、すべての \(n\ge N\) に対して \begin{equation*} | a_{n} - e | \lt 1 \end{equation*} となるような \(N\) を見つけられるはずだが、それには例えば \(N=1\) を選べばよい。(もちろん \(N=2\) でも \(N=10\) でも不等式はきちんと成り立つのでそちらを選んでもよい。) 次に \(\varepsilon=0.01\) を選んだとしよう。この場合、すべての \(n\ge N\) に対して \begin{equation*} | a_{n} - e | \lt 0.01 \end{equation*} が成り立つような \(N\) としては、例えば \(N=4\) が取れる。(\(\,|a_{4}-e|=0.009948\dots\,\)) 同様に \(\varepsilon=10^{-6}\) を取ったとすると \(N=9\) を選ぶことができる。(\(\,|a_{9}-e|\fallingdotseq3.0\times10^{-7}\,\)) このように、どんなに小さな \(\varepsilon\gt0\) を選んだとしても \(N\) を十分に大きく取りさえすれば、\(N\) より大きいすべての \(n\) に対して \(a_{n}\) と \(a\) の差を \(\varepsilon\) より小さくできるとき、その数列 \(\{a_{n}\}\) は収束すると言うのである。このような収束の定義は複雑に見えるかもしれないが、\(\infty\) という素性の知れないものが現れず、高校数学のような曖昧さがないという意味では分かりやすい。(収束性の証明は面倒になってしまうことが多いのだが…)
関数の列 \(\{f_{n}(x)\}=f_{1}(x),\,f_{2}(x),\,f_{3}(x),\,\dots\) に対しても収束の定義は通常の数列と同じである。すなわち関数の定義域内に任意の1点 \(x\) を固定したとき、任意の正の \(\varepsilon\gt0\) に対して、適当な自然数 \(N\) を取ってくれば \(n\ge N\) なるすべての自然数 \(n\) に対して \(|f_{n}(x)-f(x)|\lt\varepsilon\) とできるならば、その関数列は \(f(x)\) に収束するという。これは定義域内の任意の1点 \(x\) だけで収束を議論しているので各点収束ともいう。そして、ふつう自然数 \(N\) の値は \(\varepsilon\) だけでなく固定点 \(x\) の値にも依存する。一方、任意の \(\varepsilon\gt0\) に対して「\(x\) によらない」適当な自然数 \(N\) を定めると、任意の \(n\ge N\) と定義域内の任意の \(x\) に対して \(|f_{n}(x)-f(x)|\lt\varepsilon\) とすることができるとき \(\{f_{n}(x)\}\) はその定義域において \(f(x)\) に「一様収束」するという。
実は、連続関数列 \(\{f_{n}(x)\}\) が一様収束するとき、その収束した先の \(f(x)\) も連続関数になるという性質がある。(証明はそれほど難しくないがここでは省略する。) この対偶をとると、不連続関数に収束する連続関数列は一様収束しないと言える。すなわち式\eqref{sum}の \(f_{N}(x)\) は一様収束していないのである。実際、上のグラフで見た「ひげ」の長さは \(N\) をどんなに大きくしてもほとんど変わらず、したがって \(\varepsilon\) をひげの長さ(上の例ではおよそ \(0.18\) )よりも小さくとると、 任意の \(x\) に対して適当な \(N\) を見つけることができなくなってしまう。ただし、式\eqref{lim}にも書いたように、\(f_{N}(x)\) は各点においては \(f(x)\) に収束している(証明はしない)。不連続点の近くには「ひげ」があるため、一見その近くでは収束してないようにも見えるが、不連続点にどんなに近い \(x\) を考えても \(N\) を十分に大きく取りさえすれば、ひげはいつかその点よりも不連続点側へ移動していき、任意の精度 \(\varepsilon\) で \(f_{N}(x)\) を \(f(x)\) に近づけることができるのである(なお不連続点 \(2m\pi\)における部分和 \(f_{N}(2m\pi)\) は \(N\) の値によらずいつも \(0\) )。
関数列の一様収束性は、極限操作と積分操作の順序交換や、項別微分・項別積分可能性の条件にも関係してくるので非常に重要な性質である。(関数列の一様収束性を示すことがもともと考えていた問題よりもずっと難しくなってしまうということもよくあるのだが…)