実験データから理論式に含まれるパラメーターの値を決定するために、片対数グラフや両対数グラフにデータをプロットすることがある。例として \begin{equation} I = I_{0} \biggl( \frac{V}{V_{0}} \biggr)^{a} = b V^{a} \5 \biggl( b = \frac{I_{0}}{V_{0}^{a}} \biggr) \label{eq} \end{equation} のような電流・電圧特性をもつ系を仮定して、理論式に含まれる2つのパラメーター \(a,b\) を決定することを考えよう。指数 \(a\) を求めるためには式\eqref{eq}の対数をとるとよい: \begin{equation} \log_{10} I = a \, \log_{10} V + \log_{10} b \label{eq2} \end{equation} この式より、電流 \(I\) と電圧 \(V\) を両対数グラフにプロットすれば、その直線の傾きから \(a\) が、切片から \(b\) が求まることになる。(この問題の場合、対数の底は \(10\) である必要はなく \(2\) であっても \(e\) であっても、一貫して用いるのであれば何でもよい。ただし \(I=b\1 e^{\1aV}\) のような関係式に対しては片対数グラフを用いることになるが、例えば底が \(10\) の対数をとると \(\log_{10}I=(a\log_{10}e)V+\log_{10}b\) のように傾きに余分な因子 \(\log_{10}e\) が掛かることになるので注意しよう。) ところで、式\eqref{eq2}には電流 \(I\) や電圧 \(V\) など次元をもった物理量の対数があらわれる。物理の授業では次元をもった量の指数や対数を計算してはならないと教わるが、これはよいのだろうか? どのように解釈するべきなのだろう?
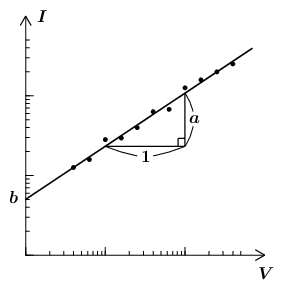
まず上の図のようなグラフを書くこと自体は問題ない。縦軸や横軸は \(\log_{10}I\) や \(\log_{10}V\) ではなく、グラフは \(I\) や \(V\) の読みをそのままプロットして描かれる。ただ単に座標軸が歪んでいるだけである。しかし、そうだとしても\eqref{eq2}のような式が書けてしまうことは問題だろう。グラフを書くこと自体に問題がなかったとしてもこれについては何も解決していない。この問題に関しては次のように考える。今、例えば \(I\) や \(V\)の単位が \(\mr{A}\) や \(\mr{V}\) であるとして \(I,V\) などはその1単位で割られていると考えるのである。式で書いたほうがわかりやすい: \begin{equation} \log_{10} \biggl( \frac{I\,[\mr{A}]}{1\,[\mr{A}]} \biggr) = a \, \log_{10} \biggl( \frac{V\,[\mr{V}]}{\,1\;[\mr{V}]} \biggr) + \log_{10} \biggl( \frac{b\,[\mr{A}/\mr{V}^{a}]}{1\,[\mr{A}/\mr{V}^{a}]} \biggr) \label{eq3} \end{equation} 勝手に追加したように見える3つの "\(1\)" だが、これらは両辺できちんとキャンセルすることに注意しよう。この式の \(I/1\) や \(V/1\)、\(b/1\) は、\(I\) や \(V\) や \(b\) がその1単位の何倍になっているかを表す量であり無次元である。式\eqref{eq2}は式\eqref{eq3}の分母の \(1\) を省略したものだと解釈する。すなわち式\eqref{eq2}の \(I\) や \(V\) や \(b\) は次元をもたない、無味乾燥な、数字としての \(I,V,b\) であると考える。
もしくは次のように考えてもよい。物理の方程式は単なる数学の方程式とはちがい、数値と次元という2つの対象に関する方程式である。例えばニュートンの運動方程式は単位をつけて \begin{equation} m \, [\mr{kg}] \ a \, [\mr{m}/\mr{s}^{2}] = F \, [\mr{N}] \label{newton} \end{equation} などと書けるが、この方程式は数値としての \(F\) の大きさが \(m\) や \(a\) に比例するという数的情報以外に、力の次元が質量と加速度の積の次元になるという次元に関する情報も併せもっている。しかしながら対数をとってグラフを書くときだけはこの次元についての情報を一時的に捨て \(ma=F\) を数値だけに関する無味乾燥な数学の方程式と見るのである。