曲率とは、曲線や曲面がどれだけ曲がっているかを表す量である。このページでは平面上の曲線 \(y=f(x)\) の曲率について考えてみよう。
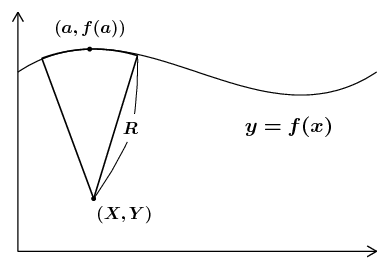
まず最初に曲率半径 \(R\) という量を導入する。曲線上の点 \((a,f(a))\) における曲率半径 \(R\) は、その点でその曲線を最もよく近似する円の半径のことをいう。ここで問題となるのは「曲線を最もよく近似する円」がどのようなものになるかだろう。これを考えるために、そのような円(曲率円という)の方程式を \begin{equation} ( x - X )^{2} + ( y - Y )^{2} = R^{2} \label{eq} \end{equation} と置くことにする。ただし \(X,Y\) は、それぞれ曲率円の中心の \(x\) 座標と \(y\) 座標である。これを \(y\) について解くと \begin{equation} y = Y \pm \sqrt{ R^{2} - ( x - X )^{2} } \end{equation} になるが、この式では1つの \(x\) に対して、2つの \(y\) が対応している(上半円・下半円)。しかし、曲率半径を考える上では、曲線 \(y=f(x)\) が上に凸か下に凸かに応じて、どちらか適当な一方の半円のみを取ればよいので、その半円を表す式を \(y=F(x)\) と置くことにしよう: \begin{equation} y = F(x) = \begin{cases} Y + \sqrt{ R^{2} - ( x - X )^{2} } \4 &( f''(x) \lt 0 ) \\[3pt] Y - \sqrt{ R^{2} - ( x - X )^{2} } &( f''(x) \gt 0 ) \end{cases} \label{eq2} \end{equation} 曲線の2階微分 \(f''(x)\) の正負に応じて場合分けが必要となるが、以下では \(F(x)\) のあらわな表式は使わないのであまり気にしなくてよい。なお、\(f''(x)=0\) の場合(直線である場合や曲線の変曲点など)についてはひとまず考えないことにする。
曲率円の方程式\eqref{eq}には円を特徴づける3つのパラメーター \(X,Y,R\) が含まれているから、曲率円に対して3つの条件を課せばこの円は一意的に定まる。その3つの条件としてはどのようなものが適切だろう? まず第一に、曲率円は問題としている曲線上の点 \((a,f(a))\) を通るべきだ。すなわち、\(x=a\) において \(F(x)\) は \(f(a)\) という値を取るべきであり、これは式で表すと \begin{equation} F(a) = f(a) \label{c1} \end{equation} となる。同様に、\(x=a\) において、曲率円 \(F(x)\) の接線の傾きは元の曲線 \(f(x)\) の接線の傾きに一致しているべきである。これは式で書くと \begin{equation} F'(a) = f'(a) \label{c2} \end{equation} となる。これで2つの条件が得られた。曲線 \(f(x)\) を直線で近似するならばこの2つの条件(点と接線の条件)だけで十分なのだが、今は円という2次曲線で近似したいわけである。そこで、\(x=a\) において、曲率円 \(F(x)\) の2階微分が曲線 \(f(x)\) の2階微分に一致するという条件も課すことにしよう。すなわち \begin{equation} F''(a) = f''(a) \label{c3} \end{equation} とする。
これで3つの条件がそろったので、あとはこの連立方程式を解いて \(X,Y\) および曲率半径 \(R\) を求めればよい。まず曲率円の方程式\eqref{eq}で \(x=a\) と置き、そこに条件\eqref{c1}を適用してみよう。条件\eqref{c1}とは、曲率円が \(x=a\) で \(y=f(a)\) を通るという条件だったから \begin{equation} ( a - X )^{2} + ( f(a) - Y )^{2} = R^{2} \label{eq3} \end{equation} となる。次に、条件\eqref{c2}を使うために式\eqref{eq}の両辺を \(x\) で微分する。式\eqref{eq2}より \(dy/dx=F'(x)\) であることに注意すると \begin{equation} ( x - X ) + ( y - Y ) \, F'(x) = 0 \label{eq4} \end{equation} になる。この式で \(x=a\) と置き、条件\eqref{c1}と\eqref{c2}を適用すれば \begin{equation} ( a - X ) + ( f(a) - Y ) \, f'(a) = 0 \label{eq5} \end{equation} を得る。最後に、条件\eqref{c3}を使うために式\eqref{eq4}の両辺をもう一度 \(x\) で微分してみよう: \begin{equation} 1 + F'(x)^{\,2} + ( y - Y ) \, F''(x) = 0 \end{equation} そして \(x=a\) を代入して条件\eqref{c1}から\eqref{c3}までをすべて使う。すると \begin{equation} 1 + f'(a)^{\,2} + ( f(a) - Y ) \, f''(a) = 0 \end{equation} が得られる。この式より \(Y\) は直ちに求まって \begin{equation} Y = f(a) + \frac{1+f'(a)^{\,2}}{f''(a)} \label{eq6} \end{equation} となる。また、この \(Y\) を式\eqref{eq5}に代入して、それを \(X\) について解けば \begin{equation} X = a - \frac{\bigl(\,1+f'(a)^{\,2}\,\bigr)\,f'(a)}{f''(a)} \label{eq7} \end{equation} が求まる。最後に式\eqref{eq6}と\eqref{eq7}を、式\eqref{eq3}へ代入すると \begin{equation} \frac{\bigl(\,1+f'(a)^{\,2}\,\bigr)^{2}f'(a)^{\,2}}{f''(a)^{\,2}} + \frac{\bigl(\,1+f'(a)^{\,2}\,\bigr)^{2}}{f''(a)^{\,2}} = R^{2} \end{equation} となるから、これを \(R\) について解いて \begin{equation} R = \frac{\bigl(\,1+f'(a)^{2}\,\bigr)^{3/2}}{|f''(a)|} \end{equation} を得る(\(\,R\) は半径なので \(R>0\) に注意)。
以上をまとめると、ある曲線 \(y=f(x)\) が与えられたとき、その曲率円の中心座標 \((X,Y)\) と曲率半径 \(R\) は \begin{align} X &= x - \frac{\bigl(\,1+f'(x)^{\,2}\,\bigl)\,f'(x)}{f''(x)} \\[8pt] Y &= f(x) + \frac{1+f'(x)^{\,2}}{f''(x)} \\[8pt] R &= \frac{\bigl(\,1+f'(x)^{\,2}\,\bigr)^{3/2}}{|f''(x)|} \end{align} となる。ただし、これまで \(a\) と書いていたものを \(x\) に置き換えた。\(X,Y,R\) は \(x\) の関数である。
これで曲率半径 \(R\) が求まった。実際に図に書いてみるとわかるが、曲率半径が大きいほど曲線の曲がり具合は小さくなるし、逆に曲率半径が小さいほど曲線はその点で大きく曲がっている。したがって、曲率半径の逆数は、曲線の曲がり具合を表す量と見ることができ、曲線 \(y=f(x)\) の曲率 \(\kappa\) を次のように定義してもよいだろう: \begin{equation} \kappa = \frac{f''(x)}{\bigl(\,1+f'(x)^{\,2}\,\bigr)^{3/2}} \end{equation} ここで曲率 \(\kappa\) は曲率半径 \(R\) の単純な逆数ではなく \(f''(x)\) にかかる絶対値を外したものとした。これにより曲率 \(\kappa\) は \(f''(x)\) と同じ符号をもつことになり、曲線が下に凸である点では \(\kappa\gt0\)、上に凸である点では \(\kappa\lt0\) となる。また、とくに \(f''(x)=0\) である点においては \(\kappa=0\) となる。そのため直線の曲率や、曲線の変曲点における曲率は \(0\) である。なお、\(f''(x)=0\) の場合には曲率半径を \(R=\infty\) と定義することにする。