単振り子の運動とヤコビの楕円関数

単振り子の運動方程式

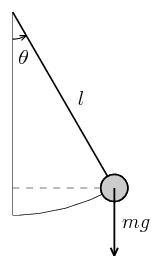
上の図のように、長さ \(l\) の軽い棒の一端を空間に固定し、他端に質量 \(m\) の質点を取り付け重力の作用により振動させることを考える。重力加速度を \(g\)、鉛直方向から測った棒の角度を \(\theta\) と置くと、質点の力学的エネルギー（運動エネルギーと位置エネルギーの和）\(E\) は \begin{equation} E = \frac{1}{2} m l^{2} \biggl( \frac{d\theta}{dt} \biggr)^{2} + mgl \, ( 1 - \cos \theta ) \label{energy} \end{equation} となる。ただし、\(\theta=0\) で位置エネルギーが \(0\) となるようにエネルギーの原点を選んだ。摩擦や空気抵抗が無視できる場合には、エネルギー保存則により \(dE/dt=0\) が成り立たなければならないから \begin{equation} \frac{dE}{dt} = m l^{2} \frac{d\theta}{dt} \frac{d^{2}\theta}{dt^{2}} + mgl \, \sin \theta \, \frac{d\theta}{dt} = 0 \end{equation} または \begin{equation} \frac{d^{2}\theta}{dt^{2}} = -\frac{g}{l} \, \sin \theta \label{motion} \end{equation} となり、一般化座標 \(\theta\) に関する運動方程式が得られる。力学の講義や普通の教科書では \(\theta\) が小さい場合だけを考え、運動方程式を \begin{equation} \frac{d^{2}\theta}{dt^{2}} \simeq -\frac{g}{l} \, \theta \end{equation} と近似し、単振動解 \begin{equation} \theta = \alpha \sin \omega t \5 \biggl( \omega = \sqrt{\frac{g}{l}} \, \biggr) \label{simple} \end{equation} を得る。しかしながら、以下では近似を用いずに運動方程式\eqref{motion}をこのままの形で解きたい。

運動方程式\eqref{motion}とエネルギー一定の式\eqref{energy}は同等だから、ここでは式\eqref{energy}を考察の出発点にしよう。エネルギー保存則より、角度 \(\theta\) の大きさが最大となるのは、質点のもつ運動エネルギーが最小となる \(d\theta/dt=0\) の時である。この時の角度を \(\alpha\) と置くことにすると（この \(\alpha\) は正でも負でもよい）、力学的エネルギーが保存することより \begin{equation} \frac{1}{2} m l^{2} \biggl( \frac{d\theta}{dt} \biggr)^{2} + mgl \, ( 1 - \cos \theta ) = mgl \, ( 1 - \cos \alpha ) \end{equation} が成り立つ。これを少し整理すると \begin{equation} \biggl( \frac{d\theta}{dt} \biggr)^{2} = 2\omega^{2} ( \cos \theta - \cos \alpha ) \end{equation} になる。ただし \(\omega=\sqrt{g/l^{\,}}\) と置いた。この式の右辺に三角関数の倍角（半角）公式 \begin{equation} 　\cos 2\theta = 1 - 2 \sin^{2} \theta, \4 \cos \theta = 1 - 2 \sin^{2} \frac{\theta}{2} \end{equation} を用いれば \begin{equation} \biggl( \frac{d\theta}{dt} \biggr)^{2} = 4\omega^{2} \biggl( \sin^{2} \frac{\alpha}{2} - \sin^{2} \frac{\theta}{2} \biggr) \end{equation} と変形される。ここで式を見やすくするため \begin{equation} k = \sin \frac{\alpha}{2} \4 ( |k| \le 1 ) \label{eq1} \end{equation} と置き、\(\theta\) から \(\phi\) への変数変換 \begin{equation} \sin \frac{\theta}{2} = k \sin \phi \label{eq2} \end{equation} を行ってみよう（\(\,\theta\le|\alpha|\) だから、この変換によって \(\sin\phi\) は \([-1,1]\) の範囲を動き、したがって \(\phi\) の変域は \([-\pi/2,\,\pi/2]\) と選べばよいことに注意）。このとき \begin{equation} \biggl( \frac{d\theta}{dt} \biggr)^{2} = 4\omega^{2} k^{2} \cos^{2} \phi \end{equation} になる。平方根を取れば \begin{equation} \frac{d\theta}{dt} = \pm 2\omega k \cos \phi \label{eq3} \end{equation} である。ところで、式\eqref{eq2}の両辺を時間 \(t\) で微分すると \begin{equation} \frac{1}{2} \, \cos \frac{\theta}{2} \, \frac{d\theta}{dt} = k \cos \phi \, \frac{d\phi}{dt} \end{equation} すなわち \begin{equation} \frac{d\theta}{dt} = \frac{2k\cos\phi}{\cos(\theta/2)} \, \frac{d\phi}{dt} = \frac{2k\cos\phi}{\sqrt{1-k^{2}\sin^{2}\phi}} \, \frac{d\phi}{dt} \end{equation} がわかるので、これを式\eqref{eq3}へ代入することで未知関数 \(\phi\) についての微分方程式 \begin{equation} \frac{d\phi}{dt} = \pm \omega \sqrt{1-k^{2}\sin^{2}\phi} \label{eq4} \end{equation} を得る。これは変数分離型だから両辺を積分することによって、少なくとも形式的には解くことができる： \begin{equation} \int \frac{1}{\sqrt{1-k^{2}\sin^{2}\phi}} \, d\phi = \pm \int \omega \, dt \end{equation} ここで左辺にある \(1/\sqrt{1-k^{2}\sin^{2}\phi}\) の原始関数の1つを \begin{equation} F(k,\sin\phi) := \int_{0}^{\phi} \frac{1}{\sqrt{1-k^{2}\sin^{2}\varphi}} \, d\varphi \5 \Bigl( |\phi| \le \frac{\pi}{2} \Bigr) \label{1st} \end{equation} という記号で表すことにすると（これを単に \(F(k,\phi)\) と書いてもよいのだが、後の議論の都合上このような形で表すことにする）、微分方程式の解は \begin{equation} F(k,\sin\phi) = \pm \omega t + C \end{equation} となる。とくに、単振動の式\eqref{simple}に対応する特解（時刻 \(t=0\) で \(\theta=0\) となる解）を考えると、式\eqref{eq2}の関係 \(\sin(\theta/2)=k\sin\phi\) より、\(\theta=0\) が \(\phi=0\) と対応することに注意して \begin{equation} F(k,\sin\phi) = \pm \omega t \end{equation} を得る。式\eqref{1st}の被積分関数が常に正であることに注意すると、複号のプラスとマイナスの違いは、\(t=0\) から少し時間が進んだときに、\(\phi\) がプラスかマイナスかの違いで、とくに式\eqref{simple}に対応する特解（\(\,t=0\) から少し時間が進んだときに、\(\theta\) の符号が \(\alpha\) や \(k\) の符号と同じ）は \begin{equation} F(k,\sin\phi) = \omega t \end{equation} で与えられる。これを \(\phi\) について解くために、\(F(k,\sin\phi)\) の変数 \(\phi\) に関する逆関数を形式的に \(\am\) という記号で表すことにすると（この \(\am\) を「振幅関数」、また \(\phi\) のことを「振幅」という） \begin{equation} \phi = \am \, \omega t \end{equation} である（振幅関数 \(\am\) はパラメーター \(k\) にも依存するため、正確には \(\am(k,\omega t)\) などと表すべきだが、以下ではとくに必要な場合を除いて引数 \(k\) は省略する）。最後に、式\eqref{eq2}の \(\theta\) と \(\phi\) の関係 \(\sin(\theta/2)=k\sin\phi\) を使って、単振り子の運動方程式の（形式的な）厳密解 \begin{equation} \theta = 2 \sin^{-1} \bigl( k \sin(\am\,\omega t) \bigr) \5 \biggl( k = \sin \frac{\alpha}{2}, \ \ \omega = \sqrt{\frac{g}{l}} \, \biggr) \label{theta} \end{equation} を得る。なお、この解は質点が \(t=0\) で \(\theta=0\) から運動を開始し、\(\theta\le|\alpha|\) の範囲で振動する特解であることに注意しよう（と言っても、\(\alpha\) または \(k\) を任意定数と見なし、\(t\to t-t_{0}\) と置き換えれば、すぐに一般解と呼べる形になるが）。

楕円積分

上で振り子の運動方程式の厳密解を書き下すことはできたが、実は式\eqref{theta}は形式的な解となる。というのも式\eqref{1st}の積分 \begin{equation} F(k,\sin\phi) = \int_{0}^{\phi} \frac{1}{\sqrt{1-k^{2}\sin^{2}\varphi}} \, d\varphi \5 \Bigl( |k| \le 1, \ \ |\phi| \le \frac{\pi}{2} \Bigr) \label{1st2} \end{equation} やその逆関数 \(\am\) は初等関数の範囲内で求められないことが知られているからである。さて、この積分\eqref{1st2}で積分変数の変換 \begin{equation} t=\sin\varphi \end{equation} を行ってみよう。このとき \begin{equation} dt = \cos \varphi \, d \varphi, \5 d\varphi = \frac{1}{\cos\varphi} \, dt = \frac{1}{\sqrt{1-t^{2}}} \, dt \end{equation} である。この変換によって \(\varphi\) の積分区間 \([\,0,\,\phi\,]\) が、\(t\) の積分区間 \([\,0,\,y\,]\) へ写るとすると（すなわち \(y=\sin\phi\,\)）、式\eqref{1st2}は \begin{equation} F(k,y) = \int_{0}^{y} \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt \5 ( |k| \le 1, \ |y| \le 1 ) \label{1st3} \end{equation} と表すこともできる。この \(F(k,y)\) や \(F(k,\sin\phi)\) を第1種楕円積分という。また、とくに \begin{equation} K(k) := F(k,1) = \int_{0}^{1} \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt = \int_{0}^{\pi/2} \frac{1}{\sqrt{1-k^{2}\sin^{2}\varphi}} \, d\varphi \end{equation} を第1種完全楕円積分という（証明は行わないが、\(k=1\) の場合を除いてこの積分は収束し、有限の値を取る）。第1種完全楕円積分も初等関数で表すことはできない。「第1種」と言うからには第2種楕円積分というものも当然あって、それは \begin{equation} E(k,y) = \int_{0}^{y} \sqrt{\frac{1-k^{2}t^{2}}{1-t^{2}}} \, dt \5 ( |k| \le 1, \ |y| \le 1 ) \end{equation} で定義される。こちらも積分変数の変換 \(t=\sin\varphi\ \,(y=\sin\phi)\) によって \begin{equation} E(k,\sin\phi) = \int_{0}^{\phi} \sqrt{1-k^{2}\sin^{2}\varphi} \ d\varphi \end{equation} という形に書き直すことができる。また第2種完全楕円積分は \begin{equation} E(k,1) = \int_{0}^{1} \sqrt{\frac{1-k^{2}t^{2}}{1-t^{2}}} \, dt = \int_{0}^{\pi/2} \sqrt{1-k^{2}\sin^{2}\varphi} \ d\varphi \end{equation} である。計算は行わないが、第2種楕円積分は楕円の弧長を計算しようとする際に現れ、パラメーター \(k\) は楕円の離心率に一致する（もし真円ならば \(k=0\,\)）。なお、楕円積分では \(k\) のことを「母数」という名前で呼ぶ。あともう1つ、第3種楕円積分というものも存在するが、物理的にはそれほど重要でないため、ここでは省略することにする。一般に、\(p(x)\) を3次または4次の多項式、\(f(x,y)\) を有理関数（2つの多項式の分数によって表されるような関数）とするときに \begin{equation} \int f\bigl(x,\textstyle{\sqrt{p(x)}}\,\bigr)\, dx \end{equation} の形の不定積分を楕円積分という。楕円積分は初等関数の範囲内で求められないことが知られているが、最終的には上で述べた3種類の標準形の和に帰着することができる。

第1種完全楕円積分を用いると単振り子の運動の1周期の長さ \(T\) を表現することができる。式\eqref{eq4}より \begin{equation} dt = \frac{1}{\omega\sqrt{1-k^{2}\sin^{2}\phi}} \, d\phi \5 \Bigl( \, \sin \frac{\theta}{2} = k \sin \phi, \ \ k = \sin \frac{\alpha}{2} \, \Bigr) \end{equation} が成り立つから、振り子の運動の \(1/4\) 周期の時間を求めるには、\(dt\) を \(0\) から \(T/4\) まで積分すればよい。このとき \(\theta\) は \(0\) から最大の角度 \(\alpha\) まで変化し、これは \(\phi\) で言うと \(0\) から \(\pi/2\) までの変化に相当する。したがって \begin{equation} \frac{T}{4} = \int_{0}^{T/4} dt = \frac{1}{\omega} \int_{0}^{\pi/2} \frac{1}{\sqrt{1-k^{2}\sin^{2}\phi}} \, d\phi \end{equation} が成り立ち、最右辺の積分は第1種完全楕円積分 \(K(k)\) の形になっているから、単振り子の運動の1周期の時間は \begin{equation} T = \frac{4K(k)}{\omega} \5 \biggl( k = \sin \frac{\alpha}{2}, \ \ \omega = \sqrt{\frac{g}{l}} \, \biggr) \end{equation} と表される。振り子の運動を単振動で近似した場合には、周期が振り子の長さ \(l\) だけで決まり \(T=2\pi/\omega=2\pi\sqrt{l/g}\) となるが、正確な計算では振動の最大角 \(\alpha\)（すなわち振幅）にも依存することがわかる。

ヤコビの楕円関数

以下では単振り子の運動で扱った第1種楕円積分に関連した数学的内容について詳しく見ていくことにしよう。前にも述べたように第1種楕円積分 \begin{equation} F(k,y) = \int_{0}^{y} \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt \5 ( |k| \le 1, \ |y| \le 1 ) \label{1st4} \end{equation} を初等関数によって表すことはできない。しかしながら、母数 \(k\) が特別な値のときにはこの積分を実行することができる。実際 \(k=0\) とすると \begin{equation} F(0,y) = \int_{0}^{y} \frac{1}{\sqrt{1-t^{2}}} \, dt \end{equation} となるが、これは変数変換 \(t=\sin\varphi\ \,(y=\sin\phi)\) によって \begin{equation} F(0,y) = \int_{0}^{\phi} d\varphi = \phi = \sin^{-1} y \end{equation} と計算され、三角関数の逆関数を使って表すことができる。そこでこれに倣い、一般の \(k\) に対しても第1種楕円積分\eqref{1st4}を使って次のような逆関数を考えることにしよう： \begin{equation} x = \int_{0}^{y} \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt = \sn^{-1} \, y \5 ( |k| \le 1, \ |y| \le 1 ) \label{1st5} \end{equation} すなわち \begin{equation} y = \sn \, x \label{sn} \end{equation} である。第1種楕円積分の逆関数として導入されたこの関数 \(\sn\,x\) は「ヤコビの楕円関数」と呼ばれるものの1つで、読んでそのまま「エスエヌ関数」と呼ばれている。前に \(F(k,\sin\phi)\) の逆関数として定義した振幅関数 \begin{equation} x = \int_{0}^{\phi} \frac{1}{\sqrt{1-k^{2}\sin^{2}\varphi}} \, d\varphi = \am^{-1} \, \phi \5 \Bigl( |k| \le 1, \ \ |\phi| \le \frac{\pi}{2} \Bigr) \label{1st6} \end{equation} \begin{equation} \phi = \am \, x \label{am} \end{equation} と同様に、\(\sn\,x\) も本来は母数を明記して \(\sn(k,x)\) などと表すべきところだが、以下ではとくに必要な場合を除いて引数 \(k\) は省略する。式\eqref{1st5}の積分の上限 \(y\) と、式\eqref{1st6}の積分の上限 \(\phi\) の間に \(y=\sin\phi\) という関係があったことを思い出すと、\(\sn\)関数と振幅関数には \begin{equation} \sn \, x = \sin ( \am \, x ) \label{snam} \end{equation} の関係があることがわかる。この性質を使うと、振り子の問題で求めた運動方程式の解\eqref{theta}は、\(\sn\)関数を使って \begin{equation} \theta = 2 \sin^{-1} ( k \, \sn \, \omega t ) \5 \Bigl( k = \sin \frac{\alpha}{2} \Bigr) \end{equation} と表現することもできる。

関数 \(y=\sn\,x\) の定義域と値域について考えてみよう。まず値域は、式\eqref{1st5}の積分が実数の範囲で値をもつ \(|y|\le1\) になるだろう。この変域 \(-1\le y\le1\) において、式\eqref{1st5}の被積分関数が常に正であることから、逆関数 \(x=\sn^{-1}\,y\) は単調に増加することがわかる。そして、その最大値は第1種完全楕円積分 \begin{equation} x_{\max} = \int_{0}^{1} \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt = K(k) \end{equation} で与えられる。最小値も完全楕円積分を使って \begin{equation} x_{\min} = \int_{0}^{-1} \! \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt = \int_{0}^{1} \frac{1}{\sqrt{(1-s^{2})(1-k^{2}s^{2})}} \, (-ds) = -K(k) \end{equation} と表される（途中で \(t\to-s\) と変数変換を行った）。まとめると \(K=K(k)\) として、\(y=\sn\,x\) の定義域は \(-K\le x\le K\)、値域は \(-1\le y\le1\) となり、\(y\) は \(x\) の関数として単調に増加する。ちなみに、\(k=0\) のときには \begin{equation} K(0) = \int_{0}^{1} \frac{1}{\sqrt{1-t^{2}}} \, dt = \int_{0}^{\pi/2} d\varphi = \frac{\pi}{2} \end{equation} となるから、三角関数 \(y=\sin x\) で言うと定義域が \(-\pi/2\le x\le\pi/2\) に制限されていることになる。証明は省略するが、\(\sin x\) が周期 \(2\pi\) の周期関数としてすべての実数で定義されたように、\(\sn\,x\) も同様の繰り返しを考えることで、周期 \(4K\) の周期関数としてすべての実数に拡張することができる（\(\,2K\) 進むごとに \(+\sn\to-\sn\to+\sn\to-\sn\to\dots\) と繰り返してやればよい）。振り子の運動方程式の解に現れた \(\sn\,\omega t\) の部分は、そのように周期関数として拡張された\(\sn\)関数と見るべきものである。

　　

　　

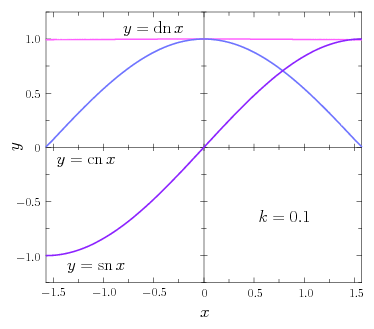
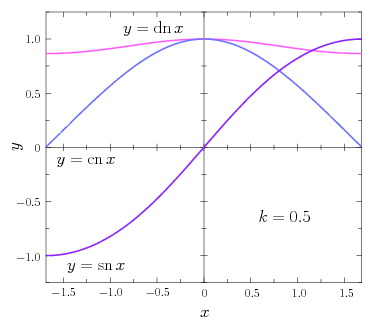
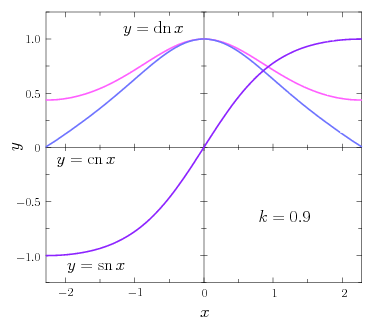
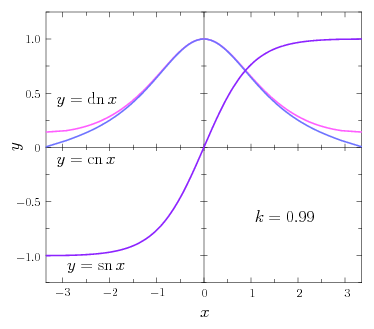
三角関数には \(\sin\) に対応して \(\cos\) という双子の兄弟がいたが、ヤコビの楕円関数においても \(\sn\) に対応して \(\cn\) という双子の兄弟がいる。この\(\cn\)関数（シーエヌ関数）は三角関数と同様に \begin{equation} \cn \, x = \sqrt{1-\sn^{2}\,x} \5 ( -K \le x \le K ) \label{cn} \end{equation} で定義され、\(\sn\)関数と同様にその適当な繰り返しを作ることですべての実数に拡張できる。この \(\cn\,x\) の定義式に式\eqref{snam}の関係を代入すると \begin{equation} \cn \, x = \sqrt{1-\sin^{2}(\am\,x)} = \cos(\am\,x) \end{equation} となるので、\(\sn\,x\) と同様に \(\cn\,x=\cos(\am\,x)\) の関係がやはり成り立っている。さて、三角関数の \(\sin,\cos\) は双子の兄弟であったが、実はヤコビの楕円関数には双子の \(\sn,\cn\) の他にもう1人兄弟がいる。三兄弟の末っ子、\(\dn\)関数（ディーエヌ関数）は次で定義される： \begin{equation} \dn \, x = \sqrt{1-k^{2}\2\sn^{2}\,x} \5 ( -K \le x \le K ) \label{dn} \end{equation} \(\dn\)関数は \(k=0\) の三角関数の世界では常に \(1\) となって見えなくなっている関数である。なお、詳しい理由は説明しないが、\(\dn\)関数を周期関数としてすべての実数に拡張したい場合には、その周期を \(2K\) とする（単純に \(+\dn\) を繰り返していけばよい）。注意すべきは、\(\dn\,x\) が三角関数の \(\tan x\) に対応するものではないということである。ヤコビの楕円関数にも \(\tan x\) に対応する \(\mr{tn}\,x=\sn\,x/\cn\,x\) という関数はあるのだが（\(\,\mr{tn}\,x\) は \(\mr{sc}\,x\) と書かれることもある）、楕円関数の世界では \(\dn\,x\) のほうがより本質的で重要となる。

\(\sn\,x,\,\cn\,x,\,\dn\,x\) はいずれもヤコビの楕円関数と呼ばれる関数たちである。しかし、単に「楕円関数」と言った場合、それはヤコビの楕円関数だけを意味してはいない。楕円関数とは一般に「複素平面上の異なる2つの方向へ周期をもつ有理型関数」という性質を備えたすべての関数を意味する言葉である（有理型関数とは有理関数のような複素関数のことで、その定義域上で極以外の特異点をもたないものをいう）。もちろん、ヤコビの楕円関数はそのような意味での楕円関数の一種になっており、ヤコビの楕円関数を複素関数へ拡張した場合には実軸以外の方向にも周期性をもつことが知られている。

ヤコビの楕円関数のいくつかの性質

ヤコビの楕円関数 \(\sn(k,x)\) は、\(k=0\) のとき \(\sn(0,x)=\sin\,x\) になったが、では \(k=1\) のときにはどのような関数になるだろう？ これを調べるために第1種楕円積分 \begin{equation} F(k,y) = \int_{0}^{y} \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt \end{equation} で \(k=1\) と置いてみよう： \begin{equation} F(1,y) = \int_{0}^{y} \frac{1}{1-t^{2}} \, dt \end{equation} この積分は初等的に計算することができて \begin{equation} F(1,y) = \frac{1}{2} \int_{0}^{y} \Bigl( \frac{1}{1+t} + \frac{1}{1-t} \Bigr) \, dt = \frac{1}{2} \biggl[ \, \ln(1+t) - \ln(1-t) \, \biggr]_{0}^{y} = \frac{1}{2} \, \ln \biggl( \frac{1+y}{1-y} \biggr) \label{1st7} \end{equation} となる。この逆関数を考えるため \begin{equation} x = \frac{1}{2} \, \ln \biggl( \frac{1+y}{1-y} \biggr) \end{equation} と置いて、\(y\) について解くと \begin{equation} y = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} = \tanh x \end{equation} を得る。すなわち \begin{equation} \sn(1,x) = \tanh x \end{equation} である。このとき\(\cn\)関数は \begin{equation} \cn(1,x) = \sqrt{1-\tanh^{2}x} = \frac{1}{\cosh x} \end{equation} となる。\(k=1\) のときには定義より \(\dn(1,x)=\cn(1,x)\) であるから、\(\dn\)関数も \begin{equation} \dn(1,x) = \frac{1}{\cosh x} \end{equation} である。これらは上で示したグラフの振る舞いにも一致するだろう。なお、\(\tanh x\) や \(1/\cosh x\) は周期関数ではないから、\(k=1\) の場合におけるヤコビの楕円関数は、正確には「楕円関数」ではない。実際、\(k=1\) のときの完全楕円積分 \(K(1)\) の値を計算しようとすると、式\eqref{1st7}より \begin{equation} K(1) = \lim_{y\to1} F(1,y) \to \infty \end{equation} となって周期が無限大になってしまう。（実は \(k=0\) の三角関数も実軸方向にしか周期的とならないため「楕円関数」ではない。そのためヤコビの楕円関数の正確な定義では母数を \(0\lt k\lt1\) の範囲に取る。） なお、振り子の運動で言うと、\(k=1\) とは、振り子が \(\theta=\pi\ (=\alpha)\) の角度へ向かって無限の時間をかけて倒立しようとする運動になる（実質的には倒立して止まってしまった状態に見える）。

最後に、ヤコビの楕円関数の導関数を求めてみよう。式\eqref{1st5}の第1種楕円積分 \begin{equation} x = \int_{0}^{y} \frac{1}{\sqrt{(1-t^{2})(1-k^{2}t^{2})}} \, dt \end{equation} は、\(y=\sn\,x\) を \(x\) について解いた式であったが、この両辺を \(y\) で微分することで \begin{equation} \frac{dx}{dy} = \frac{1}{\sqrt{(1-y^{2})(1-k^{2}y^{2})}} \end{equation} という式が得られる。これより \(y=\sn\,x\) の導関数は \begin{equation} \frac{dy}{dx} = \frac{1}{dx/dy} = \sqrt{(1-y^{2})(1-k^{2}y^{2})} = \sqrt{1-\sn^{2}\,x}\sqrt{1-k^{2}\,\sn^{2}\,x} \end{equation} となるから、\(\cn\,x,\,\dn\,x\) の定義式\eqref{cn}、\eqref{dn}を使って \begin{equation} \frac{d}{dx} \, \sn\,x = \cn\,x \, \dn\,x \end{equation} を得る。\(\cn\,x\) の導関数を求めるには、定義式\eqref{cn}を \(x\) で微分すればよい： \begin{equation} \frac{d}{dx} \, \cn\,x = \frac{d}{dx} \sqrt{1-\sn^{2}\,x} = \frac{1}{2} \frac{-2\,\sn\,x}{\sqrt{1-\sn^{2}\,x}} \Bigl( \frac{d}{dx} \, \sn\,x \Bigr) = -\frac{\sn\,x}{\cn\,{x}} \Bigl( \frac{d}{dx} \, \sn\,x \Bigr) \end{equation} ここへ先に求めた \(\sn\,x\) の微分公式を代入すれば \begin{equation} \frac{d}{dx} \, \cn\,x = -\sn\,x \, \dn\,x \end{equation} になる。\(\dn\,x\) についても同様で \begin{equation} \frac{d}{dx} \, \dn\,x = \frac{d}{dx} \sqrt{1-k^{2}\sn^{2}\,x} = \frac{1}{2} \frac{-2k^{2}\,\sn\,x}{\sqrt{1-k^{2}\sn^{2}\,x}} \Bigl( \frac{d}{dx} \, \sn\,x \Bigr) = -k^{2} \, \frac{\sn\,x}{\dn\,{x}} \Bigl( \frac{d}{dx} \, \sn\,x \Bigr) \end{equation} より \begin{equation} \frac{d}{dx} \, \dn\,x = -k^{2} \, \sn\,x \, \cn\,x \end{equation} となる。三角関数には2回微分すると（負号をつけて）元に戻るという性質があったが、ヤコビの楕円関数にはそのような簡単な性質はなく、微分するたびにどんどん複雑な形へ変化していく。