実験データをまとめる時など、我々はふだん何気なくグラフに目盛りを振ることができている。しかし、この「グラフに目盛りを振る」という作業を、例えばコンピューターでも行えるように、アルゴリズムとして表現しようとすると意外と難しい問題であることに気づく。このページではグラフの目盛り間隔を自動的に決定するアルゴリズムについて紹介しよう。
「グラフ」と言われたとき、ふつうは縦と横に \(x\) 座標と \(y\) 座標を備えた2次元的なグラフを想像するだろうか。以下で考えたいのは、もちろん、そのような普通のグラフについての問題なのだが、「目盛りを振る」という作業だけをとくに抜き出して考える場合には、別に2次元的なグラフを扱う必要はない: 目盛りを振るための作業手順は \(x\) 座標と \(y\) 座標で全く同一で、またそれぞれ独立に行うことができるものなので、\(x\) 座標(数直線)に目盛りを振る方法さえわかってしまえば、あとは座標軸が何本に増えようともやることは変わらない。そこで、以下では1次元の数直線に目盛りを振る手順について考えることにする(ここから先では数直線のことを「グラフ」と呼んだりするので注意)。

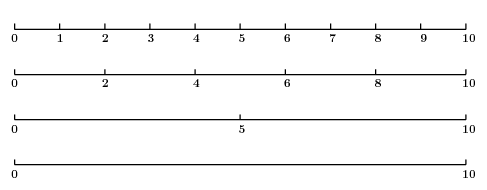
グラフに振られる目盛りの間隔は、与えられたデータの範囲に応じて実に様々である。上の図に示したように、グラフの \(x\) 座標のデータが \(0\) から \(10\) までの値を取るように変化するとき、我々は \(0,\,1,\,2,\,3,\dots,\,10\) というふうに1刻みで目盛りをつけようとするだろう。いや、人によっては \(0,\,2,\,4,\,6,\,8,\,10\) という2刻みの目盛りのほうをより好むかもしれない。それだけでなく5刻みの目盛りや0.5刻みの目盛りだって考えられる。ただ、5刻みにすると少し目盛り間隔が広すぎるような気がするし、0.5刻みになると目盛り間隔が狭くて隣り合った数字を区別しにくい感じがする。もし0.5刻みを採用するなら、\(0.5,\,1.5,\,2.5,\,\dots,\,9.5\) の目盛りには数値を伴わせず、目盛り線だけの「小目盛り」とする方法も考えられるだろうか。5刻みのグラフも小目盛りを適当に追加すればそれなりに見栄えのよいグラフになると思う。\(0\) から \(10\) までという1つのデータ範囲を考えただけでもこれだけいろいろな目盛り間隔が考えられるのに、実際にはさらに無数のデータ範囲をもった数値たちがグラフを描くためのデータとして与えられ得るのである。それは例えば \(9.95\) から \(10.00\) までという比較的狭い(?)範囲かもしれないし、逆に \(0\) から \(10^{20}\) という非常に広い範囲になるかもしれない。とても大きな数字や小さな数字が出てきたときには、座標軸の脇に「\(\times10^{n}\)」のような補助的な数字を置く必要も出てくるだろう。
このように「グラフに目盛りを振る」という作業は、与えられるデータの範囲(それは無数の可能性が考えられる!)に強く依存するものであり、また人間の美的感覚によるところもあるため、それを一般化してコンピューターでも行えるようにアルゴリズム化することは少し難しい問題であるように感じる。しかしながら、グラフの目盛り間隔にまったく何も法則性がないかというとそうではないようだ。いろいろなグラフを観察していると、どのようなグラフに対しても次のような共通点があることに気づく:
- 目盛り間隔は \(1,\,2,\,5\) の3通り、あるいはその \(10\) 倍や \(100\) 倍、\(1/10\) 倍や \(1/100\) 倍などだけである。(3刻みや7刻みで数字が増えていく目盛りは(ほとんど)存在しない。)
- 数値を伴った目盛りは最低でも2つ必要である。(もし数字の添えられた目盛りが1つまたは0であると、グラフの描かれた範囲がどれくらいの大きさであるのか判断できなくなってしまうため)
いずれの特徴もほとんど自明なことであり、わざわざ文字にして説明するまでもないことなのだが、しかしこの当たり前の2つの事実をきちんと意識しない限りは問題を解決することはできないと思う。というのも、これら2つの条件だけから目盛り間隔の最大値が一意に決定されてしまうのである。このことを具体例を交えながら見ていきたい。
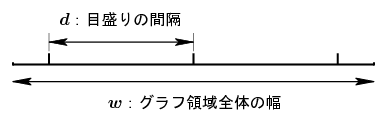
今、何かグラフを描くための数値データが与えられたとすると、そのグラフの中に少なくとも2つの目盛りが存在するための条件は \begin{equation} 2d \le w \label{eq} \end{equation} と書くことができる。ただし、\(d\) は隣り合う目盛りどうしの間隔、\(w\) はグラフ領域全体の幅を表す(下図参照)。この不等式が正しいことは、例えば下の図で \(w\) を左右から同時に狭めていったとき、\(w\lt2d\) となってしまうと真ん中の目盛り1つだけになってしまうことから理解できると思う。\(d\le w/2\) という式から目盛り間隔には上限が存在することになる。では、目盛り間隔の最大値は \(w/2\) になるかというと必ずしもそうではなく、目盛り間隔として許されるのは \(1,\,2,\,5\) に関係する数字だけであったから、そのような数の中で最大のものがグラフに振ることのできる目盛り間隔の最大値となるわけである。
具体的に、与えられたデータの範囲が \([-3,3]\) であった場合に、上の方法で目盛り間隔を計算してみよう。このときグラフ領域の幅は \(w=3-(-3)=6\) となるから、不等式\eqref{eq}より \begin{equation*} 2d \le 6 \3 \text{あるいは} \3 d \le 3 \end{equation*} が言えることになる。ところが目盛り間隔 \(d\) として許されるのは \(1,\,2,\,5\) に関係する数字だけであったから、目盛り間隔としては \begin{equation*} d = 2, \ \ 1, \ \ 0.5, \ \ 0.2, \ \ 0.1, \ \ 0.05, \dots \end{equation*} だけが候補となる。とくに許される目盛り間隔の最大値は \(d=2\) であるから、その整数倍の \(-2,\,0,\,2\) の3点に目盛りを振って座標軸が完成する。
今の例では目盛り間隔 \(d\) として最大値 \(d=2\) を採用したが、もちろん、好みに応じて \(d=1\) や \(d=0.5\) などを採用してもよい。ただ、目盛り間隔があまり細かくなりすぎると、目盛りに添えられた数字が隣どうし重なり合うようになるので、とくにコンピューターに自動的に目盛りを描画させようとする場合には、いちばん広い目盛り間隔を採用しておくのが無難である。ただし多くの場合、最大の目盛り間隔を採用すると目盛りの数が少なく殺風景な見た目のグラフとなってしまうので、もとの目盛りをさらに何分割かするような小目盛りを振るようにしておくとよいだろう。小目盛りには数字を添えないようにしておけば、隣どうし数字が重なり合うという問題も起こらない。
目盛りに添えられた数字が隣どうし重なったり、はみ出したりするという問題が発生するのは、絶対値の大きな数字や小さな数字(例えば \(100000000\) や \(0.000000001\) など)が現れた場合も同様である。そのような場合には「\(\times10^{n}\)」のような数字を座標軸のそばに置いて、目盛りに添えられる数字があまり長くなりすぎないようにすればよいだろう。