P型半導体のホール効果の謎

何が問題か？

下の図はホール効果測定を行う際の典型的な実験配置を示したイラストである。一様な磁場 \(\bm{B}\) の中に置かれた半導体試料に直流電源をつなぎ、一定の電圧をかけると、試料内に生じた電場 \(\bm{E}\) により、電荷 \(q\) のキャリアは力 \(q\bm{E}\) を受けて、その方向に移動をはじめる。この流れは試料内を流れる電流になるわけだが、このとき、速度 \(\bm{v}\) をもつようになったキャリアたちにはローレンツ力 \begin{equation} \bm{F} = q \1 \bm{v} \op \bm{B} \end{equation} も同時に働くことになる。これにより、キャリアは速度 \(\bm{v}\) と磁場 \(\bm{B}\) の両方に垂直な方向へと力を受け、下の図に描いたように、次第に試料の片側へ集まりはじめる。ここで注意すべきは、正孔 \(q\gt0\) をキャリアとするp型半導体と、電子 \(q\lt0\) をキャリアとするn型半導体で、電場による移動の向き（\(\,\bm{v}\) の向き）は互いに反対であるのだが、ローレンツ力 \(\bm{F}\) の向きは両者で共通となることである。そのため、電場および磁場に垂直な方向に発生した電圧（ホール電圧と呼ばれる）を測定することにより、試料内のキャリアがもつ電荷の正負を調べることができる（下の図のような実験配置では、試料左側の電位が右側よりも高くなっていれば正孔、逆に低くなっていれば電子だ）。なお、ローレンツ力によるキャリアの偏りが発生すると、それによってローレンツ力を打ち消すような向きへの電場が発生するようになるため、キャリアの左側への移動が永続することはなく、最終的に電場方向へのまっすぐな電流のみが残り、定常状態となって落ち着く。

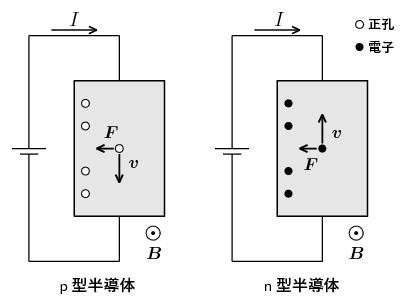
ところが、よく考えてみると上のホール効果の説明には少し不思議な点がある。正孔とは、半導体の中で電子の数が相対的に少なくなった電子の欠乏を、仮想的に正電荷の粒子と見なしたものである。p型半導体においても実際に物質内を移動している荷電粒子の実体はやはり電子なのである（正電荷の実体である陽イオンは、まわりの原子たちと固く結合しているためほとんど動けない）。そのため、ホール効果の実験における正孔の偏りを本来の電子の偏りとして図示すると下の図のようになり、p型半導体中における電子たちの移動は、上の図で見たローレンツ力 \(\bm{F}\) による移動と全く反対になってしまう…　この「本来のローレンツ力とは逆向きに働く力」こそがp型半導体におけるホール効果の謎である。もしかしたら、以上の考察で何か些細な見落としや間違いをしているのかもしれないが、この問題について何年考えても、私にはそのような間違いを見つけることはできなかった。それでは実験事実のほうがおかしいのかと言うとそれも違うようで、疑り深い私が注意深く実験してみても、やはり正孔という仮想粒子の実在を示唆するような実験結果しか得られなかった。p型半導体中の電子がローレンツ力に逆らって下の図のように移動する現象は、疑いようのない実験事実として認めるほかなさそうなのである。

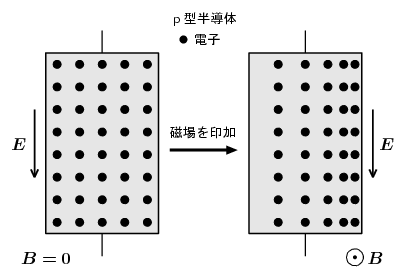
以下では、ローレンツ力と正反対の向きで電子に働く不思議な力の起源について、正孔という仮想的な粒子を導入することなく説明することができないか考察していきたい。

流体の運動方程式

これから我々が調べたいのはp型半導体の中の電子に働く奇妙な力の起源であるから、ここから先の計算に正孔という概念は一切用いたくない。そのためには正孔という仮想粒子の背景にある電子の集団を取りこぼしなく扱うことが必要になってくるが、一般的に言って、そのような多体問題を解析的に解くのはほとんど不可能なことである。そこでたくさんの電子たちをまとめて1つの連続体（流体）と見なした上での計算を行ってみることにしよう。

粘性をもたない流体（完全流体）の運動は次のオイラー方程式によって記述することができる： \begin{equation} \frac{\d\bm{v}}{\d t} + ( \bm{v} \ip \nabla ) \, \bm{v} = -\frac{1}{\rho} \nabla p + \bm{f} \label{euler} \end{equation}

この偏微分方程式は、流体力学の基礎方程式であるナビエ・ストークス方程式に、流体の粘性が入っていない特別な場合で、流体の単位体積あたりの運動量保存則から導かれる（ここで方程式の導出を行うことはしない）。未知関数は \(\bm{v},\,\rho,\,p\) の3つ（\(\,\bm{v}\) を成分に分けて書けば合計5つ）で、これらはいずれも空間座標 \(\bm{r}\) と時間 \(t\) の関数であり、それぞれ流体の速度場、密度（単位体積あたりの質量）、圧力という物理量に対応している（圧力の符号は流体が外側へ広がろうとするときに正だ）。ここで注意したいのは速度が \(\bm{v}(\bm{r},t)\) のように空間と時間の関数になっていることである。質点の力学における速度は \(\bm{v}(t)\) のように書かれ、運動する質点に貼り付いた時間 \(t\) だけの関数であったが、流体力学における速度 \(\bm{v}(\bm{r},t)\) は流体の存在する空間に貼り付いた時間と空間の関数である（電磁場や波動関数の記述法と同じ）。オイラー方程式\eqref{euler}の右辺にあるベクトル \(\bm{f}\) は流体の単位質量あたりに働く外力を表し、通常の流体力学では重力加速度 \(\bm{g}\) が入るところだが、電磁場中に置かれた電子流体の運動を考える場合には（単位質量あたりの）ローレンツ力 \begin{equation} \bm{f} = -\frac{e}{m} ( \bm{E} + \bm{v} \op \bm{B} ) \end{equation} を用いるのがよいだろう。ただし \(m\) は電子の質量、\(-e\lt0\) は電子の電荷である。これをオイラー方程式\eqref{euler}に代入すると \begin{equation} m \biggl( \frac{\d\bm{v}}{\d t} + ( \bm{v} \ip \nabla ) \, \bm{v} \biggr) = -\frac{1}{n} \nabla p - e \, ( \bm{E} + \bm{v} \op \bm{B} ) \label{euler2} \end{equation} となる。ただし \(\rho=mn\) と置いて質量密度 \(\rho\) を電子数密度 \(n\) に書き換えた。電子の運動に伴う電流密度 \(\bm{i}\) を \begin{equation} \bm{i} = -e n \bm{v} \end{equation} と簡単に表せるので、重力を扱わない今の問題では、単位体積あたりの質量 \(\rho\) よりも単位体積あたりの粒子数 \(n\) を用いた表現のほうが素直であると思う。さて、オイラー方程式\eqref{euler2}はベクトル表記で書かれているから、この式1つで3つの偏微分方程式を表すことになる。ところが未知関数は \(\bm{v},n,p\) の5つもあるから問題を解くためには方程式の数が不足しており、これらの関係を表す方程式をあと2つ探してこなければならない。必要となる残り2つのうち、1つには質量保存則 \begin{equation} \frac{\d\rho}{\d t} + \nabla \ip ( \rho \bm{v} ) = 0 \end{equation} が使われる。これは \(\rho=mn\) を使って電子数密度に書き直せば \begin{equation} \frac{\d n}{\d t} + \nabla \ip ( n \bm{v} ) = 0 \end{equation} とも表せる（この式に電子の電荷 \(-e\) をかけたものは電荷保存則である）。方程式のあと1つには熱力学的な状態方程式が使われることが多い。例えばであるが、流体が理想気体として扱える場合には、理想気体の状態方程式 \begin{equation} pV = \Bigl( \frac{N}{N_{\mr{A}}} \Bigr) RT = NkT \end{equation} を用いればよい。ただし \(V\) は流体が占める体積、\(N\) はその中の粒子数、\(T\) は流体の温度、\(N_{\mr{A}}\) はアボガドロ定数、\(k\) はボルツマン定数、\(R=N_{\mr{A}}k\) は気体定数である。この式は単位体積あたりの粒子数 \(n=N/V\) を使って \begin{equation} p = kT \1 n \label{ideal} \end{equation} と書くこともできる。半導体内の電子の熱力学的状態を記述する状態方程式としてどのようなものを用いるのが適当なのかはよくわからないが、一般に \begin{equation} p = p(n) \end{equation} のように、圧力 \(p\) と単位体積あたりの粒子数 \(n\) の間に何らかの関係式が成り立つことを仮定しておこう。（なお、多くの場合、流体の運動に伴う温度変化は小さいため、以下で温度 \(T\) は定数として扱うことにする。）

以上をまとめると、半導体内の電子を連続体として取り扱うために必要となる方程式は \begin{equation} m \biggl( \frac{\d\bm{v}}{\d t} + ( \bm{v} \ip \nabla ) \, \bm{v} \biggr) = -\frac{1}{n} \nabla p - e \, ( \bm{E} + \bm{v} \op \bm{B} ) \end{equation} \begin{equation} \frac{\d n}{\d t} + \nabla \ip ( n \bm{v} ) = 0 \end{equation} \begin{equation} p = p(n) \end{equation} の3つ（ベクトルを成分に分ければ5つ）になる。これらをホール効果の実験に対応する境界条件の下で解き、電子数密度 \(n=n(\bm{r},t)\) に電子本来のローレンツ力とは反対方向の偏りを見ることができればおもしろい。

ホール効果測定における運動方程式の解

上で導入した3つの方程式は流体の時間変化まで取り扱うことのできる一般的なものであるが、5つの未知関数を含んだ非線形の偏微分方程式であり、多くの場合この方程式を解析的に解くことは非常に難しい。しかしながら、いま我々が興味あるのは、ホール効果の実験で電流の時間的変化がなくなった定常状態における電子数密度 \(n\) だけである。定常状態における電子の速度場 \(\bm{v}\) の様子などある意味最初からわかっていて、それはたぶん電場と反対の方向を向いた時間的・空間的に一定の定数ベクトルになっているだろう。（ちなみに、典型的なp型シリコンを用いたホール効果測定では、ほとんど一瞬（1秒以内）でホール電圧の時間変化が終わり、定常的な状態に落ち着くようだ。）

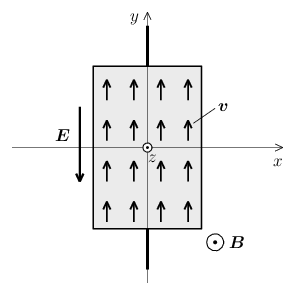
時間的に一定の定常流に対しては、運動方程式から時間微分の項が消えるので \begin{equation} m \, ( \bm{v} \ip \nabla ) \, \bm{v} = -\frac{p'(n)}{n} \nabla n - e \, ( \bm{E} + \bm{v} \op \bm{B} ) \end{equation} \begin{equation} \nabla \ip ( n \bm{v} ) = 0 \end{equation} と簡単化することができる。なお、圧力 \(p\) は状態方程式 \(p=p(n)\) が与えられていればすぐに計算できるものなので \(\nabla p=p'(n)\2\nabla n\) の関係を使って微分方程式の中からは消去した。未知関数は2本の微分方程式の中に現れる \(\bm{v}(\bm{r}),n(\bm{r})\) の2つだけと考えてよい。さて、上の図のように、直方体形の半導体試料のちょうど中心に原点を置いた \(xyz\)-座標を取ろう。そして電場と磁場の向きを \begin{equation} \bm{E} = ( \, 0, -E, \, 0 \, ), \4 \bm{B} = ( \, 0, \, 0, B \, ) \5 ( E, B \gt 0 ) \end{equation} に取る（一様な電場と磁場を考えているので \(E,B\) はいずれも定数である）。電場・磁場の向きおよび座標系をこのように定めると、\(+x\) 方向に電子が偏ったときはp型半導体的、\(-x\) 方向に電子が偏ったときはn型半導体的となるので覚えておくとよい。この時、速度と磁場の外積は \begin{equation} \bm{v} \times \bm{B} = ( \, v_{x}, v_{y}, v_{z} \, ) \times ( \, 0, \, 0, B \, ) = ( \, v_{y} B, \, -v_{x} B, \, 0 \, ) \end{equation} で与えられるから、上の微分方程式を成分に分けて書いたものは \begin{align} &m \Bigl( v_{x} \frac{\d}{\d x} + v_{y} \frac{\d}{\d y} + v_{z} \frac{\d}{\d z} \Bigr) v_{x} = -\frac{p'}{n} \frac{\d n}{\d x} - e B \2 v_{y} \\[5pt] &m \Bigl( v_{x} \frac{\d}{\d x} + v_{y} \frac{\d}{\d y} + v_{z} \frac{\d}{\d z} \Bigr) v_{y} = -\frac{p'}{n} \frac{\d n}{\d y} + e E + e B \2 v_{x} \\[5pt] &m \Bigl( v_{x} \frac{\d}{\d x} + v_{y} \frac{\d}{\d y} + v_{z} \frac{\d}{\d z} \Bigr) v_{z} = -\frac{p'}{n} \frac{\d n}{\d z} \label{eq} \end{align} \begin{equation} \frac{\d}{\d x} ( n v_{x} ) + \frac{\d}{\d y} ( n v_{y} ) + \frac{\d}{\d z} ( n v_{z} ) = 0 \end{equation} となる。ここで、もし \(v_{z}=0\) であるなら（ホール効果の実験ではおそらくそのようになっている）、式\eqref{eq}より \(\d n/\d z=0\) となるから \(n\) は \(x\) と \(y\) だけの関数であり、また残りの3つの微分方程式からも \begin{align} &m \Bigl( v_{x} \frac{\d}{\d x} + v_{y} \frac{\d}{\d y} \Bigr) v_{x} = -\frac{p'}{n} \frac{\d n}{\d x} - e B \2 v_{y} \label{eq2}\\[5pt] &m \Bigl( v_{x} \frac{\d}{\d x} + v_{y} \frac{\d}{\d y} \Bigr) v_{y} = -\frac{p'}{n} \frac{\d n}{\d y} + e E + e B \2 v_{x} \end{align} \begin{equation} \frac{\d}{\d x} ( n v_{x} ) + \frac{\d}{\d y} ( n v_{y} ) = 0 \label{eq3} \end{equation} のように \(z\) 座標に関する情報が完全に消えるため、実質的に \(x\) と \(y\) だけを座標変数とする2次元系として扱ってよいことになる \((\bm{v}=\bm{v}(x,y),\,n=n(x,y))\) 。ここまではやや一般性を保ったまま式変形を行ってきたが、最後に電子の流れが \(+y\) 方向に一定であるという条件 \begin{equation} \bm{v} = ( \, 0, \, v, \, 0 \, ) \5 ( v \gt 0 ) \label{v} \end{equation} を代入すると（\(\,v\) は定数である）、上の3つの微分方程式は \begin{equation} -\frac{p'}{n} \frac{\d n}{\d x} - e v B = 0 \label{eq4} \end{equation} \begin{equation} -\frac{p'}{n} \frac{\d n}{\d y} + e E = 0, \4 v \frac{\d n}{\d y}= 0 \label{eq5} \end{equation} という味気ない式になる。このうち式\eqref{eq5}の2つの式から \begin{equation} E = 0 \end{equation} が導かれることになるが、これは半導体試料内に\(-y\) 方向の一様な電場が発生しているという前提条件に矛盾する。このことは式\eqref{v}の \(\bm{v}\) が微分方程式\eqref{eq2}-\eqref{eq3}の解にはなり得ないことを意味し、そのため式\eqref{v}に代わるより適切な \(\bm{v}\) を探してこなければならない　……が、しかし、よく考えてみると式\eqref{v}の仮定よりも、\(E\gt0\) という前提条件のほうが信用できない気もする。現実の半導体試料に一定の電圧をかけた時、その内部に一定の電場が発生しているという確証はない。もしかしたら半導体を構成する原子たちが分極を起こすなどして、その中を移動する電子たちが感じる電場は実効的に \(0\) になっているのかもしれない。また、電気伝導についての古典的な Drude モデルにおいては、伝導電子が物質内で衝突を繰り返すことにより、電場とは反対方向に、平均すると電場による力と同じだけの大きさの抗力を受けるとされている。そもそも、ニュートン力学で一定速度の運動というのは、何も外力が存在していない状況において実現されるものだ（\(\,\bm{F}=-e\bm{E}\) という一定の力が働いている場合の運動は時間に比例して速度を増していくような運動となる）。今我々が探したいのは速度や電流が一定の状態に落ち着いたあとの定常的な解であった。

そこで、この先では運動方程式のほうを信じて、少なくとも電流の時間的変化がなくなった定常状態においては \(E=0\) が実効的に成り立っていることを仮定しよう。幸い、これまで \(E\gt0\) であるという条件はどこにも用いていないので、ここまでの式は \(E=0\) と置けばそのまま使うことができる。このとき式\eqref{v}の \(\bm{v}\) は微分方程式の解になる資格があり、また式\eqref{eq5}より電子数密度 \(n\) は \(x\) だけの関数となる。そして式\eqref{eq4}は常微分方程式 \begin{equation} \frac{p'(n)}{n} \frac{dn}{dx} = -e v B \label{eq6} \end{equation} に変わる。この微分方程式は変数分離形なので直ちに積分することができて \begin{equation*} \int \frac{p'(n)}{n} \, dn = -e v B \int dx \end{equation*} より \begin{equation} P(n) = -e v B \1 x + C \end{equation} という解を得る。ただし、\(n\) の関数 \(P(n)\) は \(p'(n)/n\) の原始関数の1つで \begin{equation} P'(n) = \frac{p'(n)}{n} \end{equation} を満足するものとする。積分定数 \(C\) の値を決めるために、境界条件として試料の中心 \((x=0)\) における電子数密度 \(n=n(0)\) を \(n_{0}\) と置くことにすれば、\(C=P(n_{0})\) に定まるので \begin{equation} P(n) - P(n_{0}) = - e v B \1 x \label{eq7} \end{equation} となる。

最後に \(n=n(x)\) の形で表すため少し近似を行ってみたい。\(n_{0}\) 近傍の \(P(n)\) の変化があまり大きくない範囲において \begin{equation} n = n_{0} + \varDelta n \end{equation} と置くことにすれば \begin{equation*} P(n) - P(n_{0}) \simeq P'(n_{0}) \, \varDelta n = \frac{p'(n_{0})}{n_{0}} \varDelta n \end{equation*} と近似できるので \begin{equation} \frac{\varDelta n}{n_{0}} = -\frac{evB}{p'(n_{0})} \, x \end{equation} または \begin{equation} n(x) = \biggl( 1 - \frac{evB}{p'(n_{0})} \, x \biggr) n_{0} \label{n} \end{equation} という線形近似式を得る。これ以上の考察は状態方程式 \(p=p(n)\) を与えた上で行うことにしよう。

理想気体の状態方程式を用いたモデル

より具体的な計算を行うために、上で得た解に理想気体の状態方程式を適用して考察を行っていく。半導体内の電子に理想気体の状態方程式を適用することがどれほど意味のあることか分からないが、何も行わないよりはよいだろう。

電子流体の状態方程式として式\eqref{ideal}に与えた理想気体の状態方程式 \begin{equation} p = kT \1 n \end{equation} を採用してみよう。この場合 \begin{equation} p(n) = kT \1 n, \4 p'(n) = kT \end{equation} より \begin{equation} P(n) = \int \frac{p'(n)}{n} \, dn = kT \int \frac{dn}{n} = kT \ln n \end{equation} となるから、これを式\eqref{eq7}に適用して \begin{equation} kT \ln \Bigl( \frac{n}{n_{0}} \Bigr) = -e v B \1 x \end{equation} あるいは \begin{equation} n(x) = n_{0} \exp \Bigl( -\frac{evB}{kT} \, x \Bigr) \end{equation} という電子数密度を得る。定数 \(n_{0},e,v,B,k,T\) はいずれも正なので、この関数は \(x\) の単調減少関数であり、半導体の右側 \((x\gt0)\) よりも左側 \((x\lt0)\) のほうで電子の数が多く、n型半導体におけるホール効果を表しているようである。残念ながらp型半導体に対応したホール効果にはならなかったが、電子の移動に伴ってローレンツ力の向きに電荷の偏りが発生するという現象は、流体の方程式を用いても再現できることが分かった。

せっかくなので、半導体試料の両側でどの程度の電荷密度の変化が発生するか計算してみよう。試料に加える磁場を \(B=0.03\,\mr{T}\)（フェライト磁石程度）、温度を室温 \(T=300\,\mr{K}\) とし、まずは \begin{equation} \frac{evB}{kT} \end{equation} という量を評価する。電子の速さの見積もりには移動度の式 \begin{equation} v = \mu E \end{equation} を使ってみよう。具体的な数値として、p型シリコンの典型的な移動度 \(\mu=500\,\mr{cm}^{2}/(\mr{V}\ip\mr{s})\) と、通常ホール効果の実験で用いられる程度の電場（電圧）の大きさ \(E=5\,\mr{V}/\mr{cm}\) を用いて計算を行えば \begin{equation*} \frac{e\mu EB}{kT} = 0.29 \, \mr{cm}^{-1} \end{equation*} という値になる。このとき \(x\) 方向に \(1\,\mr{cm}\) の幅をもつ半導体試料の電子密度は、左端 \((x=-0.5\,\mr{cm})\) で \begin{equation*} n = n_{0} \exp \bigl( -0.29 \times ( -0.5 ) \bigr) = n_{0} \exp(0.145) = 1.156 \, n_{0} \end{equation*} また、試料の右端 \((x=+0.5\,\mr{cm})\) で \begin{equation*} n = n_{0} \exp(-0.145) = 0.865 \, n_{0} \end{equation*} という値を取る。すなわち、試料の中心 \((x=0)\) と比べて、試料の左端では \(+15.6\,\%\)、右端では \(-13.5\,\%\) の電子数密度の増減が生じたことになる。この数字を見ると、ホール効果の通常の実験条件の範囲内で、指数関数をテイラー展開の1次までで近似することはほどほどに有効な近似であり、式\eqref{n}の線形近似 \begin{equation} n \simeq \biggl( 1 - \frac{evB}{p'(n_{0})} \, x \biggr) n_{0} = \biggl( 1 - \frac{evB}{kT} \, x \biggl) n_{0} \end{equation} を用いてもそれなりの精度で電子数密度の変化を知ることができる。

ところで、この式の中の \(x\) の係数の符号を反転させることはできるだろうか？ もしそれができたなら、電子数密度の増加・減少の関係がこれまでと正反対になるので、当初の目的であったp型半導体的な電子数密度の変化が得られることになる。これは理想気体の状態方程式を用いた場合の話であるが、より一般的な状況においても、式\eqref{eq6}から \begin{equation} \frac{dn}{dx} = -\frac{evB}{p'(n)} n \end{equation} という関係式が得られるので、やはり \(-evB/p'(n)\) という部分の符号から電子数密度の増減を知ることができる。ところが今の問題設定では常に \(e,v,B\gt0\) であるから、\(n(x)\) の傾きを変えるには \(p'(n)\) の符号を変えるほかない。ただ、理想気体の状態方程式を考える限りは常に \(p'(n)=kT\gt0\) であるため、そのようなことは起こらないし、そもそも、電子数密度が増加するにしたがって逆に圧力が減少するなどあり得ないことのように思えるが…

ファンデルワールスの状態方程式を用いたモデル

理想気体の状態方程式に分子間力と気体分子の大きさの効果を取り入れて修正したものとして、ファンデルワールスの状態方程式 \begin{equation} \biggl( p + a \frac{(N/N_{\mr{A}})^{2}}{V^{2}} \biggr) \biggl( V - b \Bigl( \frac{N}{N_{\mr{A}}} \Bigr) \biggr) = \Bigl( \frac{N}{N_{\mr{A}}} \Bigr) R T \end{equation} がある。定数 \(a,\) は気体の分子間に働く引力（ファンデルワールス力）を、定数 \(b\) は気体分子の大きさの効果（体積排除効果）を反映したパラメーターである。0でない大きさをもつ分子間に引力が働くとする通常の実在気体を扱う限りは \(a,b\gt0\) であるが、もし \(a=b=0\) としたなら、それは上で考察してきた理想気体の状態方程式に一致する。以下ではファンデルワールスの状態方程式を採用して計算を行ってみたい。

まず、ファンデルワールスの状態方程式を \(p=p(n)\) の形に直してみよう。示量変数である粒子数 \(N\) と体積 \(V\) を粒子数密度 \(n=N/V\) の形にまとめると \begin{equation} \biggl( p + \frac{a}{N_{\mr{A}}^{2}} n^{2} \biggr) \biggl( 1 - \frac{b}{N_{\mr{A}}} n \biggr) = kT \1 n \end{equation} となるので \begin{equation} p(n) = \frac{kT\1n}{1-(b/N_{\mr{A}})n} - \frac{a}{N_{\mr{A}}^{2}} n^{2} \end{equation} を得る。体積排除効果 \(b\) は、電子流体を扱う限りは差し当たり \(b=0\) としてもよいだろうか（素粒子である電子は現在のところ大きさをもたない点粒子と考えられている）。その場合、圧力の関数形は \begin{equation} p(n) = kT \1 n - \alpha n^{2} \5 \biggl( \alpha = \frac{a}{N_{\mr{A}}^{2}} \biggr) \end{equation} という簡単な形になる。そして、この \(p(n)\) を電子数密度の線形近似式\eqref{n}に代入すれば \begin{equation} n(x) = \biggl( 1 - \frac{evB}{p'(n_{0})} \, x \biggr) n_{0} = \biggl( 1 - \frac{evB}{kT-2\alpha n_{0}} \, x \biggr) n_{0} \label{n2} \end{equation} になる。電子流体を理想気体として扱うモデルにおいては \(\alpha=0\) であり、常に \(x\) の減少関数（n型半導体的）であったが、今考えているモデルでもし \begin{equation} kT - 2\alpha n_{0} \lt 0 \4 \text{または} \4 \alpha \gt \frac{kT}{2n_{0}} \end{equation} となるようなことがあれば、これは \(x\) の増加関数（p型半導体的）になる。実在気体においてパラメーター \(\alpha\) または \(a\) は分子間に働く引力を表すものだったから、もし半導体内の電子間に強い「引力」が働いているならこのようなことが起こり得るだろう。ふつうに考えて、同符号の電荷をもつ電子間に引力が働くことなどあり得ないが、半導体内に存在する電子の背後には正電荷をもった多数の陽イオンも存在しているわけで、これら陽イオンとのクーロン相互作用までを加味した実効的な電子間相互作用にはもしかしたら「引力」が働いているのかもしれない。なお、実在気体の分子間力は常に引力であるため \(\alpha\gt0\) であるが、半導体内の電子の場合、電子間には斥力が働くこともあるかもしれない。そのような場合には \(\alpha\lt0\) とすることで斥力を表現することもできるだろう。個人的には、そのような場合がn型半導体に相当するのではないかと思っている。また、相互作用が何もない場合、すなわち \(\alpha=0\) の場合には、理想気体モデルでの結果がそのまま使えるので、そのような物質の振る舞いはn型半導体的となることが予想される。電子を理想気体モデル（自由電子モデル）で扱ってよい固体とは金属のことだが、これは多くの金属がn型を示すという実験事実と整合する。ちなみに、もし \begin{equation*} 2 |\alpha| n_{0} \gg kT \end{equation*} となるようなことがあれば、式\eqref{n2}は \begin{equation*} \varDelta n = \frac{evB}{2\alpha} \, x \end{equation*} と近似されるため、\(\alpha\) の符号の正負（p型かn型か）とホール電圧の符号の正負がきれいに一致することになる。ただ、厳密には \(kT\) の項が存在していて、その分だけn型半導体のホール電圧やキャリア密度は大きめに、逆にp型半導体ではそれらが小さめに評価されることになる。このことは、p型半導体よりもn型半導体で移動度（\(\propto\,\)ホール電圧）の絶対値が大きく出やすいという実験事実ともうまく整合しているように見える。

最後に、p型半導体内の電子間に働く引力のパラメーター \(a\) の大きさを見積もってみよう。上のモデルによると、p型半導体的なホール電圧が発生するための条件は \begin{equation} \alpha \gt \frac{kT}{2n_{0}} \4 \text{または} \4 a \gt \frac{N_{\mr{A}}^{2}kT}{2n_{0}} \end{equation} であるが、これに室温 \(T=300\,\mr{K}\) と、半導体と呼ばれるような物質のキャリア密度の典型的な値 \(n_{0}=10^{20}\text{～}\,10^{25}\ \mr{m}^{-3}\) を代入してみると \begin{equation*} a \gt 10^{2} \, \text{～} \, 10^{7} \ \mr{Pa} \ip \mr{m}^{6} \end{equation*} という値を得る。これは実在気体に対する \(a\) の実測値（分子間力の小さなヘリウムでは \(3.45\times10^{-3}\,\mr{Pa}\ip\mr{m}^{6}\)、分子間力の大きな水蒸気でも \(5.53\times10^{-1}\,\mr{Pa}\ip\mr{m}^{6}\) 程度）と比較して非常に大きいから、もしかすると、以上の考察はまったく見当違いのものになるかもしれない。けれども素朴に考えて、気体分子間に働く分子間力よりも半導体内の電子間に働く相互作用のほうがずっと強いだろうから、実在気体に比べて大きな値の \(a\) が出たということ自体は理にかなったことだと思う。

以上をまとめると、流体の運動方程式によって半導体内電子を連続体として取り扱うモデルが正しいとするなら、p型半導体内の電子たちをローレンツ力とは反対の方向へ移動させている力の起源は、電子間に働く「引力」ということになる。この「引力」は、電子たちの背景にある陽イオンまで含めた実効的なクーロン場によってもたらされたものであると推測される。

p型半導体やn型半導体に対するこれまでの伝統的な解釈は、もしかしたら修正されるべきものなのかもしれない。これまで、キャリアが正孔であるものをp型半導体、キャリアが電子であるものをn型半導体と呼んで区別してきたが、このページでのホール効果に対する解釈が正しければ、伝導電子間に引力の働くものがp型半導体、斥力の働くものがn型半導体という区別になりそうである。p型半導体であってもn型半導体であっても、伝導電子の集団が電場（電流）と反対の方向へ一斉に移動していくことに変わりはなく、p型半導体に対してだけ「電子の抜け穴を他の電子が埋めていく」という不自然な電気伝導機構を導入する必要はなくなる。