複素数の指数関数・対数関数・べき関数

極形式と偏角

\(x\) と \(y\) を実数とするとき、実数 \(x\) と虚数 \(iy\) との形式的な和 \(z=x+iy\) を複素数という。下の図のように任意の複素数に対して \(xy\)-平面上の点を1対1に対応させることができるが、このような複素数を対応させた2次元平面を「複素平面」または「ガウス平面」とよぶ。

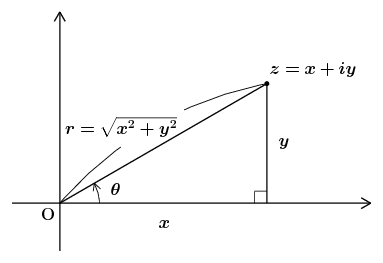
複素数 \(z\) と原点 \(\mr{O}\) との距離 \(r=\sqrt{x^{2}+y^{2}}\) を \(z\) の絶対値といい \(|z|\) で表す。すなわち \begin{equation} |z| = r = \sqrt{ x^{2} + y^{2} } \end{equation} である。また上の図に示した角度 \(\theta\) を用いると、\(0\) でない複素数 \(z\) に対して \begin{equation} z = x + iy = r \, \Bigl( \frac{x}{r} + i \frac{y}{r} \Bigr) = r \, ( \cos \theta + i \sin \theta ) \label{polar} \end{equation} という表し方ができる。\(r\) と \(\theta\) を使ったこの表式を極形式とよぶ。また \(\theta\) を \(z\) の偏角とよび \begin{equation} \theta = \arg z \end{equation} と書くことがある。（注意：\(z=0\) である場合には \(z\) の偏角は考えない。絶対値は \(|z|=0\) である。） いま \(\theta\) をあたかも1つの数のように扱ったが、式\eqref{polar}からわかるとおり \(\theta\) には \(2\pi\) の整数倍の不定性がある。\(\theta\) のとり得る値のうちの1つを \(\theta_{0}\) と置くことにすると（\(\,\theta_{0}\) はある1つの実数） \begin{equation*} \theta = \{ \, \theta_{0} + 2\pi n \ | \ n = 0, \pm1, \pm2, \dots \, \} \end{equation*} である。\(\theta\) を数で表そうとすると数の集合になる（この集合記号を用いた表記はあまり一般的でないので注意）。ところで \(\theta\) の値が1つに決まっていたほうが便利なこともある。そういう場合には \(\theta\) の値を、例えば \(0\le\theta\lt2\pi\) などに制限することがあり、そのようにして1つに定まった \(\theta\) を \begin{equation} \theta = \Arg z \end{equation} と表し偏角の「主値」とよぶ。この式では \(\theta\) は集合ではなく1つの数を表していることに注意しよう。\(\theta\) と書くと集合なのか、1つの数なのかまぎらわしいので、以下では偏角を表す記号としてできるだけ \(\arg z\) や \(\Arg z\) という書き方を用いるようにしたい。

なお \(\Arg z\) の範囲は文脈によって変わる。上では \(0\le\Arg z\lt2\pi\) のように書いたが、\(-\pi\lt\Arg z\le\pi\) であることもあるし \(-\pi/2\lt\Arg z\le3\pi/2\) となることもある。一般的な議論をする場合には \(\Arg z\) の範囲が明示されないこともあるが、そのような場合には適当な1つの範囲が想定されているのだと考えればよい。

練習問題として \(z=r(\cos\theta+i\sin\theta)\) の逆数の絶対値と偏角を計算してみよう。\(1/z\) を極形式で表すと \begin{align} \frac{1}{z} &= \frac{1}{r(\cos\theta+i\sin\theta)} \notag \\[5pt] &= \frac{1}{r} ( \cos \theta - i \sin \theta ) \notag \\[5pt] &= \frac{1}{r} \bigl( \cos (-\theta) + i \sin (-\theta) \bigr) \label{reciprocal} \end{align} となるので \begin{equation} \Biggl| \frac{1}{z} \Biggr| = \frac{1}{|z|}, \4 \arg \Bigl( \frac{1}{z} \Bigr) = -\arg z \end{equation} がわかる。

複素数の指数関数

複素数 \(z=x+iy\) の指数関数 \(e^{z}\)（\(\1\exp z\) と書くこともある）を \begin{equation} e^{z} = e^{x+iy} := e^{x} ( \cos y + i \sin y ) \label{expz} \end{equation} で定義する。（記号 \(:=\) は、記号の左側にあるものを右側で定義するという意味。\(\equiv\) を使うこともあるが、どちらをどちらで定義しているのかが曖昧なので \(:=\) や \(=:\) と書いたほうが明確である。） 無限級数によって \begin{equation*} e^{z} = \sum_{n=0}^{\infty} \frac{z^{n}}{n!} \end{equation*} と定義することも多いが、いくつかの性質の証明が簡単になるし、なによりも直観的にわかりやすいため、ここでは式\eqref{expz}を指数関数の定義とする（実はどちらの定義式を使っても同じ性質が導かれる）。まだいまのところは底が \(e\) 以外の指数関数については全く未知であることに注意しよう。式\eqref{expz}が複素数の指数関数の自然な定義であることは次のようにして確かめられる。まず \(y=0\) と置けば通常の実数の指数関数 \(e^{x}\) に一致する。また2つの複素数 \(z_{1}=x_{1}+iy_{1}\) と \(z_{2}=x_{2}+iy_{2}\) を考え、それらの指数関数の積を計算すると \begin{align*} e^{z_{1}} e^{z_{2}} &= e^{x_{1}} ( \cos y_{1} + i \sin y_{1} ) \cdot e^{x_{2}} ( \cos y_{2} + i \sin y_{2} ) \\[3pt] &= e^{x_{1}+x_{2}} \bigl( ( \cos y_{1} \cos y_{2} - \sin y_{1} \sin y_{2} ) + i ( \sin y_{1} \cos y_{2} + \cos y_{1} \sin y_{2} ) \bigr) \\[3pt] &= e^{x_{1}+x_{2}} ( \cos ( y_{1} + y_{2} ) + i \sin ( y_{1} + y_{2} ) ) \\[3pt] &= e^{z_{1}+z_{2}} \end{align*} となるから（途中で三角関数の加法定理を使った）、指数法則 \begin{equation} e^{z_{1}} e^{z_{2}} = e^{z_{1}+z_{2}} \label{exp} \end{equation} が成立していることもわかる。式\eqref{expz}でとくに \(x=0\) の場合、つまり \(z\) が純虚数のときを考えると \begin{equation} e^{iy} = \cos y + i \sin y \label{euler} \end{equation} という等式が得られるが、これを「オイラーの公式」という。オイラーの公式を用いると極形式\eqref{polar}は \begin{equation} z = r e^{i\theta} \end{equation} のように簡便に記述することができる。式\eqref{expz}を極形式\eqref{polar}と比べると、\(e^{z}=e^{x+iy}\) の絶対値と偏角が \begin{equation} | e^{z} | = e^{x}, \4 \arg e^{z} = \{ \, y + 2\pi n \ | \ n = 0, \pm1, \pm2, \dots \, \} \label{expz2} \end{equation} によって与えられることがわかる。偏角の主値の範囲を適当に選べば \(\Arg e^{z}=y\) となる。

練習問題として複素数 \(z=re^{i\theta}\) の整数乗を計算してみよう。指数法則\eqref{exp}を使うと \(z^{2}\) は \begin{equation*} z^{2} = z \cdot z = r e^{i\theta} \cdot r e^{i\theta} = r^{2} e^{2i\theta} \end{equation*} となる。同様にして \(z^{3}\) は \begin{equation*} z^{3} = r^{3} e^{3i\theta} \end{equation*} となり、一般に \begin{equation} z^{m} = r^{m} e^{im\theta} \end{equation} が言える。すなわち \(z^{m}\) の絶対値は \(z\) の絶対値の \(m\) 乗、偏角は \(z\) の偏角の \(m\) 倍（に \(2\pi\) の整数倍を足したもの）となる。

複素数の対数関数

指数関数 \(e^{z}\) の逆関数、対数関数について考えよう。複素関数 \(f(\cdot)\) の逆関数とは、複素 \(z\) 平面（の部分集合）上の各点を \(w=f(z)\) によって複素 \(w\) 平面上へ移したとき、その \(w\) 平面（の部分集合）上の点1つ1つを、\(z\) 平面の対応する元の点1つ1つへきれいに返すような操作 \(z=f^{-1}(w)\) における \(f^{-1}(\cdot)\) のことである。今の場合、\(w=e^{z}\) によって \(z\) 平面から \(w\) 平面へ移った点の1つ1つを元にもどす関数 \(z=\log w\) のことだ。式\eqref{expz}を見て少し考えるとわかるが、指数関数 \(e^{z}\) は \(z\) 平面全体を \(w\) 平面上の原点を除いた領域へ移す。したがって、原点をのぞく \(w\) 平面上の任意の点を、\(w=e^{z}\) を満足するように \(z\) 平面全体へもどす規則が対数関数となる。その規則を見つけるために \(w=e^{z}\) の両辺を極形式で次のように書き表してみよう： \begin{equation*} |w| \, e^{i\arg w} = e^{x} \1 e^{iy} \5 ( z = x + iy ) \end{equation*} そして、この式の絶対値部分と偏角部分をそれぞれ比較すると \begin{equation*} x = \ln |w|, \4 y = \arg w \end{equation*} であることがわかる。したがって \(w=e^{z}\) の逆関数 \(z=\log w\) は \begin{equation*} \log w = \ln |w| + i \arg w \end{equation*} で与えられることになる。（この式の右辺は数字（実部）と集合のようなもの（虚部）の足し算という少し奇妙な形になっているが、ベクトルで書いた式と同じように複数の式をまとめて表現したものなのだと解釈しよう。） \(w\) を \(z\) へ書き換えると、対数関数 \(\log z\) とは原点を除く全複素平面で定義された次のような関数となる： \begin{equation} \log z = \ln |z| + i \arg z \5 ( z \neq 0 ) \label{logz} \end{equation} \(\log z\) の虚部には \(z\) の偏角 \(\arg z\) が含まれているが、これは \(\log z\) が1つの複素数ではなく複素数の集合であることを意味している。集合のような記号を使って表すと \begin{equation*} \log z = \{ \, \ln |z| + i ( \Arg z + 2\pi n ) \ | \ n = 0, \pm1, \pm2, \dots \, \} \end{equation*} である。虚部 \(\arg z\) の影響はたとえ \(z\) が正の実数であったとしても残る。実際、正の実数 \(z=x\gt0\) に対して上の式は \begin{equation*} \log x = \{ \, \ln x + 2\pi i n \ | \ n = 0, \pm1, \pm2, \dots \, \} \end{equation*} となるが、これは高校までに習ってきた対数関数とは明らかにちがう。虚部が存在するし、そもそも1つの数ではない！ したがって複素平面の原点以外で定義された（複素）対数関数は、正の実数に対してのみ定義された通常の（実）対数関数とは明確に区別する必要がある。そこで以下では（というよりもこのサイトでは）通常の実関数としての対数関数には \(\ln\) という記号を、複素関数としての対数関数には \(\log\) という記号を使うことにする。すなわち \(\ln x\) と書いた場合、それはいつも1つの数に対応しているが、\(\log z\) と書いた場合、それはいつも式\eqref{logz}のような無限集合を表すものとする。（なお複素関数論では底が \(e\) 以外の対数を用いることはほぼない。したがって \(\log_{10}\) のように底を明示的に記した場合には実数の対数を表すものとしよう。） ところで、偏角 \(\arg z\) に対してはその範囲を制限した主値 \(\Arg z\) というものを考えたが、対数関数 \(\log z\) に対しても、その虚部 \(\arg z\) の主値をとって1つの数を採用することがある。普通はそれを \(\Log z\) で表し、その値を主値とよぶ： \begin{equation} \Log z := \ln |z| + i \1 \Arg z \end{equation}

対数関数の話の最後に、\(\log z\) はいつも無限多価だが、それを指数関数の肩に乗せた \(e^{\log z}\) はいつも一価であることに注意しよう。実際計算してみると \begin{equation*} e^{\log z} = e^{ \ln |z| + i ( \Arg z + 2\pi n ) } = e^{ \ln |z| + i \1 \Arg z } e^{ 2\pi i n} \5 (n = 0, \pm1, \pm2, \dots) \end{equation*} となるが、オイラーの公式\eqref{euler}からすべての整数 \(n\) に対して \begin{equation*} e^{ 2\pi i n} = \cos ( 2\pi n ) + i \sin ( 2\pi n ) = 1 \end{equation*} であるので、多価性をもたらす部分はきれいに消えてしまう。一方で、\(e^{z}\) の対数 \(\log e^{z}\)は無限多価になる。実際、上で求めた \(e^{z}\) の絶対値と偏角\eqref{expz2}を用いて計算を行うと \begin{align} \log e^{z} &= \ln |e^{z}| + i \arg e^{z} \notag \\[3pt] &= \ln e^{x} + i ( y + 2\pi n ) \notag \\[3pt] &= x + iy + 2\pi i n \notag \\[3pt] &= z + 2\pi i n \9 ( n = 0, \pm1, \pm2, \dots ) \end{align} になる。

複素数のべき関数

\(\alpha(\neq0),\,\beta\) を任意の複素数として \(\alpha\) の \(\beta\) 乗を次で定義する： \begin{equation} \alpha^{\beta} := e^{ \beta \log \alpha } \4 ( \alpha \neq 0 ) \end{equation} この式は、実数 \(a\,(\gt0),\ b\) に対して \(a^{b}=e^{b\ln a}\) が成り立つことに対応する。これより \(\alpha\) を任意の複素数として複素数のべき関数 \(z^{\alpha}\) を \begin{equation} z^{\alpha} = e^{ \alpha \log z } \4 ( z \neq 0 ) \label{zalpha} \end{equation} と定義できる。定義式に対数関数 \(\log z\) が入ってることから予想されるように複素数のべき関数は一般に無限多価である。しかし \(\alpha\) の値によってはそうならないこともあり（例えば \(z^{2}\) や \(z^{-1}\) を多価関数として扱ったことはないはずだ）、ここではその条件を調べることにする。対数関数の多価性をもたらす部分を分離して書いてみると（以下ではいつも \(n=0,\pm1,\pm2,\dots\) とする） \begin{equation} z^{\alpha} = e^{ \alpha \1 ( \ln |z| + i \1 \Arg z + 2\pi i n ) } = e^{ \alpha \1 ( \ln |z| + i \1 \Arg z ) } e^{ 2\pi i n \alpha } \label{zalpha2} \end{equation} となるから、不定性因子 \(e^{2\pi in\alpha}\) の部分を見ることで \(z^{\alpha}\) の多価性に関する情報を得ることができる。まず \(\alpha\) が実数で整数の場合、つまり \(\alpha=m=0,\pm1,\pm2,\dots\) の場合を考えると \begin{equation*} e^{ 2\pi i n m } = \cos ( 2\pi n m ) + i \sin ( 2\pi n m ) = 1 \end{equation*} より \(z^{m}\) は一価になることがわかる。そして、その絶対値と偏角は \begin{equation*} z^{m} = e^{ m \1 ( \ln |z| + i \1 \Arg z ) } = e^{ m \ln|z| } e^{ i m \2 \Arg z } = |z|^{m} e^{ i m \2 \Arg z } \end{equation*} より \begin{equation} |z^{m}|=|z|^{m} \end{equation} \begin{equation} \arg z^{m}= m \2 \Arg z + 2\pi \1 l \4 ( \1 l = 0, \pm1, \pm2, \dots ) \end{equation} となる。べき関数の定義\eqref{zalpha}によって複素数の整数乗の計算方法がこれまでと変わることはない。例えば \(z\) の3乗を計算したければ \(z\) 同士を3回掛け合わせればよいのである。

次に \(\alpha\) が実数で有理数である場合、すなわち \(p,q\) を互いに素な整数として既約分数表示 \(\alpha=q/p\ \ (p\gt0)\) で与えられる場合を考えよう。このとき不定性因子は \begin{equation*} e^{ 2\pi i n \alpha} = e^{ 2\pi i n q/p } = \cos \Bigl( 2\pi \frac{qn}{p} \Bigr) + i \sin \Bigl( 2\pi \frac{qn}{p} \Bigr) \5 ( n = 0, \pm1, \pm2, \dots ) \end{equation*} であるが、このうち \(n\) を変えたときに相異なるのは \(n=0,1,\dots,p-1\) に対応する \(p\) 通りだけである（なぜならば、これら \(p\) 個のうちの任意の2つの偏角の差が \(2\pi\) の整数倍になることはなく、またこの \(p\) 個以外のものに対しては、もとの \(p\) 個の中に偏角の差が \(2\pi\) の整数倍となるようなものが必ず存在しているから）。したがって \(z^{q/p}\) は \(p\) 個の異なった値を取る \(p\) 価関数である。そしてその絶対値と偏角は \begin{align*} z^{q/p} &= e^{ (q/p) ( \ln |z| + i \1 \Arg z + 2\pi i n ) } \\[3pt] &= \sqrt[\scriptstyle p]{|z|^{q}} \, e^{ i (q/p) ( \Arg z + 2\pi n) } \5 ( n = 0, 1, \dots, p-1 ) \end{align*} より \begin{equation} |z^{q/p}| = \sqrt[\scriptstyle p]{|z|^{q}} \end{equation} \begin{align} \arg z^{q/p} = \Bigl( \frac{q}{p} \Bigr) \Arg z + \Bigl( \frac{2\pi q}{p} \Bigr) n + 2\pi \1 l \5 ( \1 l = 0, \pm1, \pm2, \dots ) \end{align} で与えられる。（以下、根号 \(\sqrt[\scriptstyle p]{\mathstrut\ \ }\) を用いて \(1/p\) 乗を表した場合は非負実数に対して定義された素朴な意味での \(1/p\) 乗を表すものとし、その計算結果は一価・非負実数としよう。） 複素数の有理数乗による多価性は偏角の部分にのみ現れ、絶対値は共通となる。

\(\alpha\) が整数や有理数以外の場合、すなわち無理数や虚部をもった複素数である場合には \(z^{\alpha}\) はいつも無限多価になる。試しにその絶対値と偏角を計算してみよう。\(a,b\) を実数として \(\alpha=a+ib\) と置くと \begin{align} z^{\alpha} &= e^{ \alpha \log z} \notag \\ &= e^{ ( a + ib ) ( \ln |z| + i \arg z ) } \notag \\ &= e^{ ( a \ln |z| - b \arg z ) + i \1 ( b \ln |z| + a \arg z ) } \notag \\ &= |z|^{a} e^{-b \arg z} \cdot e^{ i \1 ( b \ln |z| + a \arg z ) } \label{zalpha3} \end{align} であるから \begin{equation} \begin{split} |z^{\alpha}| &= |z|^{a} e^{-b\arg z} \\ &= |z|^{a} e^{-b\,(\Arg z+2\pi n)} \end{split} \end{equation} \begin{equation} \begin{split} \6 \arg z^{\alpha} &= b \ln |z| + a \arg z + 2\pi \1 l \\[3pt] &= b \ln |z| + a \, ( \Arg z + 2\pi n ) + 2\pi \1 l \5 ( \1 l = 0, \pm1, \pm2, \dots ) \end{split} \end{equation} を得る（ここで \(|z|^{a}\) は実数の実数乗による素朴な意味でのべき乗を表すものとしよう）。 \(b\neq0\) である場合、\(z\) の偏角の任意性 \(n=0,\pm1,\pm2,\dots\) によって \(|z^{\alpha}|\) は無限個の値をとる。また、たとえ \(b=0\) であったとしても \(a\) が無理数であるなら、\(n\) の選び方によって \(\arg z^{\alpha}\) は無限個の異なる値をとる。なお、\(l\) は \(z^{\alpha}\) の偏角の不定性であり多価性とは関係ない。

一般の指数関数

底が \(e\) でない一般の指数関数は \begin{equation} \alpha^{z} = e^{ z \log \alpha } \4 ( \alpha \neq 0 ) \label{alphaz} \end{equation} となる。これは \begin{equation} \alpha^{z} = e^{ z \, ( \ln |\alpha| + i \1 \Arg \alpha +2\pi i n ) } \4 ( n = 0, \pm1, \pm2, \dots ) \label{alphaz2} \end{equation} と書くことで、べき関数と同じ無限多価関数のように見えるが、正確にはそうではない。べき関数\eqref{zalpha2}の無限多価性は \(z\) の偏角の不定性がもたらしたものであり、関数に引数があってはじめて現れる。一方、指数関数\eqref{alphaz2}がもつ無限に多くの値は \(\alpha\) の偏角の不定性からきており、引数 \(z\) の存在によらず関数自身が最初からもつ性質である。その意味で指数関数\eqref{alphaz2}は無限に多くの関数、関数の集合をまとめて表したものと言える。集合記号を使って書くと \begin{equation*} \alpha^{z} = \{ \, e^{ z \, ( \ln |\alpha| + i \1 \Arg \alpha +2\pi i n ) } \ | \ n = 0, \pm1, \pm2, \dots \, \} \5 \text{（関数の集合）} \end{equation*} である。\(n\) の値を1つ定めるごとに決まる集合の要素の1つ1つはそれぞれ一価関数であることに注意しよう（底が \(e\) の指数関数だけは特別に一価関数なのである）。指数関数 \(\alpha^{z}\) は無限に多くの一価関数を表している。（一方、先ほどのべき関数 \(z^{\alpha}\) はただ1つの多価関数を表している。）

ところでこのページの最初のほう、式\eqref{expz}で指数関数 \(e^{z}\) を定義したが、それは無限に多くの関数ではなくただ1つの関数を表していた。この意味を考えるために式\eqref{alphaz}の定義にしたがい指数関数の底 \(\alpha\) が \(\mr{e}=2.71828\dots\) である場合を計算してみよう。（1つの複素数としての自然対数の底をアップライト \(\mr{e}\) で表すことにする。） \begin{equation*} \mr{e}^{z} = e^{ z \log \mr{e} } = e^{ z ( \ln \mr{e} + i \arg \mr{e} ) } = e^{z} \cdot e^{ iz \arg \mr{e} } \end{equation*} この式は無数にある \(\mr{e}\) の偏角 \(\arg\mr{e}=\{\,0,\pm2\pi,\pm4\pi,\dots\,\}\) に応じて無限に多くの関数を表すが、とくに主値 \(\Arg\mr{e}=0\) を選んだとき、それは式\eqref{expz}で定義した指数関数 \(e^{z}\) に一致する。実は指数関数 \(e^{z}\) とは、無限個の要素をもつ関数の集合 \(\mr{e}^{z}\) の中からもっとも自然な形をした1つを採用したものである。

一般に、無限個の関数を同時に扱うことは不便だし、多くの場合そうしなければならない理由もあまりないため、「指数関数」と言った場合には \(\alpha\) の偏角の主値を適当に選んでおいて、ただ1つの関数 \begin{equation} \alpha^{z} = e^{z\,\Log\alpha} \4 ( \alpha \neq 0 ) \end{equation} だけを扱うことにするのがふつうである。

複素数の指数・対数の性質

このページの最後に、複素数の指数や対数についての性質をいくつかまとめておく。実数のときと同じ式が成り立つこともあればそうでないこともあるので、複素数の指数や対数が現れる計算ではいつも丁寧な計算を行うように心がけよう。

まず最初に偏角の基本的な性質を示しておく。2つの複素数 \(\alpha\) と \(\beta\) を極形式で表し、その積を計算すると \begin{equation*} \alpha \beta = |\alpha| e^{ i \arg \alpha } \, |\beta| e^{ i \arg \beta } = | \alpha \beta | \, e^{ i( \arg \alpha + \arg \beta ) } \end{equation*} となるから \begin{equation} \arg ( \alpha \beta ) = \arg \alpha + \arg \beta \label{arg} \end{equation} がわかる。しかし、次は必ずしも成り立たない： \begin{equation} \Arg ( \alpha \beta ) = \Arg \alpha + \Arg \beta \4 \text{（正しくない）} \label{arg2} \end{equation} 例えば、偏角の主値を \(0\le\theta\lt2\pi\) の範囲に制限して \(\alpha=\beta=e^{\pi i}\) である場合を考えると、\(\Arg\alpha=\Arg\beta=\pi\) であるが、\(\Arg(\alpha\beta)=\Arg e^{2\pi i}=0\) となり \(\Arg\alpha+\Arg\beta=2\pi\) には一致しない。式\eqref{arg}を使うと対数の性質 \begin{equation} \log ( \alpha \beta ) = \log \alpha + \log \beta \label{log} \end{equation} を示せる。実際 \begin{align*} \log ( \alpha \beta ) &= \ln | \alpha \beta | + i \arg ( \alpha \beta ) \\[3pt] &= \ln |\alpha| + \ln |\beta| + i \arg \alpha + i \arg \beta \\[3pt] &= \log \alpha + \log \beta \end{align*} となる。しかし、式\eqref{arg2}が正しくないことから次は必ずしも成立しない： \begin{equation} \Log ( \alpha \beta ) = \Log \alpha + \Log \beta \5 \text{（正しくない）} \end{equation}

指数法則\eqref{exp}は、底が \(e\) でない一般の場合には注意が必要となる。 \begin{equation} \alpha^{\beta} \alpha^{\gamma} = \alpha^{\beta+\gamma} \5 \text{（正しくない）} \label{exp2} \end{equation} なぜならば、左辺は \begin{align*} \6 \alpha^{\beta} \alpha^{\gamma} &= e^{\beta\log\alpha} \, e^{\gamma\log\alpha} \\ &= e^{\beta\1(\Log\alpha+2\pi il)} \, e^{\gamma\1(\Log\alpha+2\pi im)} \\ &= e^{(\beta+\gamma)\,\Log\alpha+2\pi i(l\beta+m\gamma)} \6 ( \1 l, m = 0, \pm1, \pm2, \dots ) \end{align*} となるのに対して、右辺は \begin{align*} \6 \alpha^{\beta+\gamma} &= e^{(\beta+\gamma)\log\alpha} \\ &= e^{(\beta+\gamma)\,\Log\alpha+2\pi in(\beta+\gamma)} \5 ( n = 0, \pm1, \pm2, \dots ) \end{align*} となるため、一般に式\eqref{exp2}両辺の集合が一致するとは限らないからである。ただし、\(l=m=n\) の場合、すなわち無数にある \(\alpha\) の偏角の中から一貫して1つの値だけを採用する場合には、一価の、1つの数に対しての等式として式\eqref{exp2}は正しいものとなる： \begin{equation} \alpha^{\beta} \alpha^{\gamma} = \alpha^{\beta+\gamma} \4 \text{（主値を使ってべき乗を一価で計算する場合は正しい）} \end{equation} 同じことだが、無限個の要素をもつ指数関数の集合 \(\alpha^{z}=e^{z\log \alpha}\) の中からただ1つの関数 \(e^{z\,\Log\alpha}\) のみを選んできた場合には指数法則が成り立つ： \begin{equation} \alpha^{z_{1}} \alpha^{z_{2}} = \alpha^{z_{1}+z_{2}} \5 ( \alpha^{z} = e^{z\,\Log\alpha} ) \end{equation} この特別な場合が \(e^{z}\) の指数法則\eqref{exp}である。一方、次の形の指数法則は（両辺にある集合が一致するという意味で）正しい： \begin{equation} ( \alpha \beta )^{\gamma} = \alpha^{\gamma} \beta^{\gamma} \label{exp3} \end{equation} なぜならば、式\eqref{log}を使って \begin{equation*} ( \alpha \beta )^{\gamma} = e^{\gamma\log(\alpha\beta)} = e^{\gamma\2(\log\alpha+\log\beta)} = e^{\gamma\log\alpha} e^{\gamma\log\beta} = \alpha^{\gamma} \beta^{\gamma} \end{equation*} となるからである。しかし主値 \(\Arg\alpha,\,\Arg\beta,\,\Arg(\alpha\beta)\) を使って一価として計算する場合、式\eqref{exp3}は必ずしも正しい等式とはならないので注意しよう。

べき関数 \(z^{\alpha}\) の対数を計算してみよう。\(\alpha=a+ib\) と置いて式\eqref{zalpha3}を利用すると \begin{align*} \log z^{\alpha} &= \ln \, ( |z|^{a} e^{-b \arg z} ) + i ( b \ln |z| + a \arg z + 2\pi n ) \\[3pt] &= a \ln |z| - b \arg z + i ( b \ln |z| + a \arg z + 2\pi n ) \\[3pt] &= ( a + ib ) \ln |z| + i ( a + ib ) \arg z + 2\pi i n \\[3pt] &= ( a + ib ) ( \ln |z| + i \arg z ) + 2\pi i n \\[3pt] &= \alpha \log z + 2\pi i n \end{align*} となる。したがって \begin{equation} \log z^{\alpha} = \alpha \log z + 2\pi i n \5 ( n = 0, \pm1, \pm2, \dots ) \label{logpow} \end{equation} である。実数の対数にはない余分な項 \(2\pi in\) がつくことに注意しよう（実数の対数ではいつも \(n=0\,\)）。ただし、この余分な項を無視しても差し支えない特別な場合がある。式\eqref{logpow}の右辺にある \(\log z\) を実部と虚部に分解して書くと \begin{align*} \log z^{\alpha} &= \alpha \, ( \ln |z| + i \1 \Arg z + 2\pi i m ) + 2\pi i n \\[5pt] &= \alpha \Bigl( \ln |z| + i \1 \Arg z + 2\pi i \Bigl( m + \frac{n}{\alpha}\Bigr) \Bigr) \5 ( m, n = 0, \pm1, \pm2, \dots ) \end{align*} となるが、とくに \(\alpha=1/p\ \ (p=\pm1,\pm2,\dots)\) という形の場合には、\((m+n/\alpha)=(m+pn)\) の部分が \(0,\pm1,\pm2,\dots\) という値をとる。（そしてそれ以外の値はとらない。） したがって \(\alpha=1/p\) のとき \begin{equation*} \log z^{1/p} = \frac{1}{p} \, ( \ln |z| + i \1 \Arg z + 2\pi i l ) \5 ( \1 l = 0, \pm1, \pm2, \dots ) \end{equation*} と書いてよく \begin{equation} \log z^{1/p} = \frac{1}{p} \log z \4 ( p = \pm1, \pm2, \dots ) \label{logpow2} \end{equation} が成り立つ。式\eqref{reciprocal2}より、とくに \(p=-1\) の場合 \begin{equation} \log \, \Bigl( \frac{1}{z} \Bigr)= -\log z \end{equation} が成り立つ。

最後に次の形の指数法則が必ずしも成立しないことを示す： \begin{equation} ( z^{\alpha} )^{\beta} = ( z^{\beta} )^{\alpha} = z^{ \alpha \beta } \5 \text{（正しくない）} \label{exp4} \end{equation} まず定義より \begin{equation*} z^{ \alpha \beta } = e^{ \alpha \beta \log z } \end{equation*} であるが、式\eqref{logpow}を利用すると \((z^{\alpha})^{\beta}\) は \begin{equation*} ( z^{\alpha} )^{\beta} = e^{ \beta \log z^{\alpha} } = e^{ \beta ( \alpha \log z + 2\pi i n ) } = e^{ \alpha \beta \log z } e^{ 2\pi i n \beta } \end{equation*} となる。同様に \begin{equation*} ( z^{\beta} )^{\alpha} = e^{ \alpha \beta \log z } e^{ 2\pi i n \alpha } \end{equation*} であるから3つの式はすべて異なっている。したがって式\eqref{exp4}は正しくない。ただし \(\alpha,\beta\) がともに整数である場合には最後の余分な因子 \(e^{2\pi in\alpha}\) や \(e^{2\pi in\beta}\) が \(1\) となるため正しい等式となる： \begin{equation} ( z^{m} )^{n} = ( z^{n} )^{m} = z^{mn} \5 m,n: \text{整数} \end{equation} なお、括弧の外側にある指数が整数であれば不定性因子が \(1\) となるため \begin{equation} ( z^{\alpha} )^{m} = z^{m\alpha} \5 m: \text{整数} \label{exp5} \end{equation} は常に成り立つ。（しかし指数の入れ替え \((z^{\alpha} )^{m}=(z^{m} )^{\alpha}\) はまちがいである。） また、括弧の内側にある指数が \(1/p\ \ (p=\pm1,\pm2,\dots)\) という形をしている場合には、式\eqref{logpow2}より \begin{equation*} \bigl( z^{1/p} \bigr)^{\alpha} = e^{\alpha\log z^{1/p}} = e^{(\alpha/p)\log z} \end{equation*} となるので \begin{equation} \bigl( z^{1/p} \bigr)^{\alpha} = z^{\alpha/p} \5 ( p = \pm1, \pm2, \dots ) \label{exp6} \end{equation} が成り立つ。式\eqref{exp5}と式\eqref{exp6}の性質を合わせると、とくに次が成り立つことになる： \begin{equation} \frac{1}{z^{\alpha}} = (z^{\alpha})^{-1} = z^{-\alpha} = (z^{-1})^{\alpha} = \Bigl( \frac{1}{z} \Bigr)^{\alpha} \end{equation} すなわち2つの指数のうちのどちらかが \(-1\) であるときには式\eqref{exp4}のような計算を行ってよい。

以上、いくつかの例を見てきてわかったと思うが、複素数の複素数乗という計算では直観的に成立しそうな式がまちがいとなることがある。ただし、整数乗は比較的よい振る舞いをすることが多く、とくに \(-1\) 乗という演算は \(1\) 乗（それは何もしないということだが）と同じくらいによい性質をもっている。