ガンマ関数の遠方における近似式(漸近展開)を使って、統計力学でよく用いられるスターリングの公式を導出してみよう。ガンマ関数の漸近展開の導出法として一般によく知られている方法では、その計算過程に複数回の近似があらわれるため導出法としてなんとなく怪しいところがあるのだが、このページで紹介する方法ではテイラー多項式による近似を1回用いるだけなので、近似計算として怪しいところがなく、近似の意図も明瞭になっていると思う。
ガンマ関数の基本的な性質
スターリングの公式はガンマ関数の漸近展開から導出される。この節ではガンマ関数の基本的な性質について復習するが、すでによく知っている人は次の節まで読み飛ばしてよい。
\(\alpha\gt0\) とするとき、ガンマ関数は次の積分で定義される: \begin{equation} \varGamma(\alpha) = \int_{0}^{\infty} t^{\alpha-1} e^{-t} \, dt \5 ( \alpha \gt 0 ) \label{gamma} \end{equation} ガンマ関数は、一般の複素数 \(\alpha\)(ただし \(\Re\alpha\gt0\,\))についても上の積分で定義されるが、このページでは簡単のため \(\alpha\) が実数の場合だけを取り扱うことにしよう。(なお \(\alpha\) の値として複素数をゆるす場合、べき関数 \(t^{\alpha-1}\) は \(\Arg\1t=0\) の分枝をとって計算するように定義されている。そのためガンマ関数は複素関数としても一価である。) ガンマ関数のもっとも重要な性質は次である: \begin{equation} \varGamma(\alpha+1) = \alpha \2 \varGamma(\alpha) \label{gamma2} \end{equation} この性質は定義式\eqref{gamma}に部分積分を行うことで簡単に示せる: \begin{align*} \varGamma(\alpha+1) &= \int_{0}^{\infty} t^{\alpha} e^{-t} \, dt \\[3pt] &= \Bigl[ -t^{\alpha} e^{-t} \Bigr]_{0}^{\infty} + \int_{0}^{\infty} \alpha \2 t^{\alpha-1} e^{-t} \, dt \\[3pt] &= \alpha \2 \varGamma(\alpha) \end{align*} とくに \(\alpha\) が自然数 \(n\) の場合には、式\eqref{gamma2}を次々と使うことによって \begin{align*} \varGamma(n+1) &= n \, \varGamma(n) \\[3pt] &= n \2 ( n - 1 ) \, \varGamma(n-1) \\ &\4 \2 \vdots \\ &= n \2 ( n - 1 ) \dotsm 2 \cdot 1 \cdot \varGamma(1) \end{align*} となるが \begin{equation*} \varGamma(1) = \int_{0}^{\infty} e^{-t} \, dt = \Bigl[ -e^{-t} \Bigr]_{0}^{\infty} = 1 \end{equation*} であるので \begin{equation} \varGamma(n+1) = n! \label{fact} \end{equation} という性質がわかる。ガンマ関数は階乗を一般化した関数である。\(\alpha=1/2\) の場合には \begin{equation} \varGamma \Bigl( \frac{1}{2} \Bigr) = \sqrt{\pi\1} \label{half} \end{equation} という値を取る。これは次のようにして証明することができる。式\eqref{gamma}で \(\alpha=1/2\) とすると \begin{equation*} \varGamma \Bigl( \frac{1}{2} \Bigr) = \int_{0}^{\infty} \frac{1}{\sqrt{t\:}} e^{-t} \, dt \end{equation*} になるが、ここで変数変換 \(\sqrt{t\:}=x\) を行うと、\(dt/dx=2x\) より \begin{equation*} \varGamma \Bigl( \frac{1}{2} \Bigr) = \int_{0}^{\infty} \frac{1}{x} e^{-x^{2}} \frac{dt}{dx} \, dx = 2 \int_{0}^{\infty} e^{-x^{2}} dx = \int_{-\infty}^{\infty} e^{-x^{2}} dx \end{equation*} となる。そして、これにガウス積分の公式 \begin{equation} \int_{-\infty}^{\infty} e^{-ax^{2}} \, dx = \sqrt{\frac{\pi}{a}} \5 ( a \gt 0 ) \label{gauss} \end{equation} を用いれば式\eqref{half}が得られる。式\eqref{half}をガンマ関数の性質\eqref{gamma2}と合わせることによって、半整数の点におけるガンマ関数の値(すなわち半整数の階乗)が計算できる。
ガンマ関数の漸近形
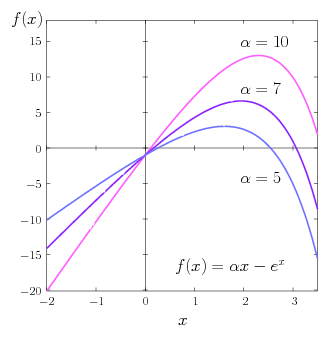
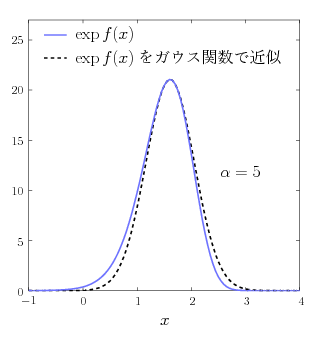
ガンマ関数の定義式\eqref{gamma}に変数変換 \(t=e^{x}\) を行ってみよう。この変換によって積分区間はすべての実数となり、また \(dt/dx=e^{x}\) より \begin{align} \varGamma(\alpha) &= \int_{0}^{\infty} t^{\alpha-1} e^{-t} \, dt \notag \\[5pt] &= \int_{-\infty}^{\infty} e^{x(\alpha-1)} \exp ( -e^{x} ) \ e^{x} dx \notag \\[5pt] &= \int_{-\infty}^{\infty} \exp ( \alpha x - e^{x} ) \, dx \label{gamma3} \end{align} となる。(個人的に、この表式がガンマ関数の最も自然な積分表示だと思っている。というのも、この表現ではべき関数の多価性が現れない。) ここで関数 \(f(x)\) を \begin{equation} f(x) = \alpha x - e^{x} \4 ( \alpha \gt 0 ) \end{equation} で定義する。この \(f(x)\) の導関数たちは簡単に求めることができて \begin{align*} f'(x) &= \alpha - e^{x} \\[8pt] f^{(k)}(x) &= -e^{x} \4 ( k \ge 2 ) \end{align*} となる。これより \(f(x)\) は、\(x=\ln\alpha\) で最大値 \(f(\ln\alpha)=\alpha\ln\alpha-\alpha\) をとり、\(x\lt\ln\alpha\) では \(-\infty\) に向かって単調に減少、\(x\gt\ln\alpha\) では \(-\infty\) に向かって指数関数的に単調減少となることがわかる。したがって、式\eqref{gamma3}の被積分関数 \(\exp f(x)\) は、\(x=\ln\alpha\) で最大値 \((\alpha/e)^{\alpha}\) をとり、\(x\to-\infty\) では指数関数的に \(0\) へ収束、\(x\to+\infty\) では二重指数関数的に \(0\) へ収束することになる。\(x\gt\ln\alpha\) における \(\exp f(x)\) の振る舞いは二重指数関数的であるから、\(x\) の増加に伴い非常に急速に減少し \(0\) へ収束する。一方、\(x\lt\ln\alpha\) における \(\exp f(x)\) の減少は通常の指数関数的な減少 \(e^{\alpha x}\) になるが、もし \(\alpha\gg1\) であるならば、こちらも急速に減少し \(0\) へ収束すると見てよいだろう。そこで、以下では \(\alpha\gg1\) を仮定し、式\eqref{gamma3}の積分を近似的に計算することを考える(積分\eqref{gamma3}を解析的に実行することはできない)。\(\exp f(x)\) が大きな値をもつのは \(x=\ln\alpha\) の近傍だけであるから、\(f(x)\) を \(\ln\alpha\) のまわりでテイラー展開してみよう: \begin{equation} f(x) = ( \alpha \ln \alpha - \alpha ) - \frac{\alpha}{2!} ( x - \ln \alpha )^{2} - \frac{\alpha}{3!} ( x - \ln \alpha )^{3} - \frac{\alpha}{4!} ( x - \ln \alpha )^{4} - \dotsb \label{taylor} \end{equation} そして、近似計算に \((x-\ln\alpha)\) の2次の項までを用いることにすると \begin{equation} \exp f(x) = \exp ( \alpha x - e^{x} ) \simeq \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \exp \Bigl( -\frac{\alpha}{2} ( x - \ln \alpha )^{2} \Bigr) \end{equation} となる。そして、この近似式を式\eqref{gamma3}へ代入すれば \begin{align*} \varGamma(\alpha) &\sim \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \int_{-\infty}^{\infty} \exp \Bigl( -\frac{\alpha}{2} ( x - \ln \alpha )^{2} \Bigr) \, dx \\[5pt] &= \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \int_{-\infty}^{\infty} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx \\[5pt] &= \sqrt{\frac{2\pi}{\alpha}} \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \end{align*} を得る。ただし、途中で変数変換 \(x\to x+\ln\alpha\) を行い、最後にはガウス積分の公式\eqref{gauss}を使った。これがガンマ関数の漸近形であり、スターリングの公式はここからすぐに導くことができる。\(\alpha\) を \(x\) に置き換えて書けば \begin{equation} \varGamma(x) \sim \sqrt{\frac{2\pi}{x}} \Bigl( \frac{x}{e} \Bigr)^{x} \5 ( x \gg 1 ) \label{asympt} \end{equation} である。
スターリングの公式
ガンマ関数の性質\eqref{gamma2}より \(\varGamma(x+1)=x\2\varGamma(x)\) であるから、式\eqref{asympt}を \(x\) 倍した次の形もガンマ関数の漸近形としてよく用いられる: \begin{equation} \varGamma(x+1) \sim \sqrt{2\pi x} \, \Bigl( \frac{x}{e} \Bigr)^{x} \5 ( x \gg 1 ) \end{equation} 多くの教科書では、こちらの形の式が先に導出されるようである。この式でとくに \(x\) が自然数 \(n\) の場合を考えると、ガンマ関数と階乗の関係\eqref{fact}より \begin{equation} n! \sim \sqrt{2\pi n} \, \Bigl( \frac{n}{e} \Bigr)^{n} \label{stirling} \end{equation} という式を得る。これがスターリングの公式である。統計力学では、この式の両辺の自然対数をとった形がよく用いられる: \begin{equation} \ln n! \sim n \ln n - n + \frac{1}{2} \ln ( 2 \pi n ) \end{equation} \(n\) が大きいときには、右辺の \(\displaystyle \frac{1}{2}\ln(2\pi n)\) はそのほかの項に比べて無視できるから、これを省略すると \begin{equation} \ln n! \sim n \ln n - n \end{equation} になる。この関係式はとくによく使われるので覚えておくとよい。
ところで、前節において求めた近似式\eqref{asympt}で \(x=n+1\) と置くと \begin{equation} n! \sim \sqrt{\frac{2\pi}{n+1}} \Bigl( \frac{n+1}{e} \Bigr)^{n+1} = \sqrt{2\pi(n+1)} \frac{1}{e} \Bigl( \frac{n+1}{e} \Bigr)^{n} \label{stirling2} \end{equation} になるから、階乗に対する2つの近似式\eqref{stirling}と\eqref{stirling2}は異なった形になっている。しかし、この相違は \(n\) が大きいときにはそれほど重要でない。式\eqref{stirling2}を少し変形すると \begin{equation*} n! \sim \sqrt{2\pi(n+1)} \frac{1}{e} \Bigl( \frac{n}{e} \Bigr)^{n} \Bigl( 1 + \frac{1}{n} \Bigr)^{n} \end{equation*} になるが、\(n\gg1\) のとき \begin{equation*} \sqrt{n+1} = \sqrt{n\1} \, \sqrt{ 1 + \frac{1}{n} } \simeq \sqrt{n\1} \end{equation*} であることと、自然対数の底の定義式 \begin{equation*} \lim_{n\to\infty} \Bigl( 1 + \frac{1}{n} \Bigr)^{n} = e \end{equation*} を用いると、\(n\) が十分大きいときには、式\eqref{stirling}と式\eqref{stirling2}がほぼ等しい値を取ることがわかる。
下の表に2種類の近似式による \(n!\) の計算値を示す。もともとは \(n\) が大きいことを仮定して導いた近似式であったが、\(n\) の小さなところでもほどほどによい値を返していることがわかるだろう。また近似式\eqref{stirling}、近似式\eqref{stirling2}のいずれも真値に対していつも小さめの値を返している。近似式\eqref{stirling2}を用いた計算のほうが若干精度がよいが、スターリングの公式として代数的に利用したい場合には、近似式\eqref{stirling}のほうがシンプルな形で扱いやすい。
| \(n\) | \(n!\) | 近似式\eqref{stirling} | 近似式\eqref{stirling2} |
|---|---|---|---|
| \(1\) | \(1\) | \(0.9221370\) | \(0.9595022\) |
| \(2\) | \(2\) | \(1.9190044\) | \(1.9454032\) |
| \(3\) | \(6\) | \(5.8362096\) | \(5.8765438\) |
| \(4\) | \(24\) | \(23.506175\) | \(23.603834\) |
| \(5\) | \(120\) | \(118.01917\) | \(118.34636\) |
| \(10\) | \(3628800\) | \(3598695.6\) | \(3601420.5\) |
ガンマ関数の漸近展開
上で求めたガンマ関数の漸近形はいつも真値よりすこし小さめの値を返していた。以下では式\eqref{taylor}のテイラー展開において無視された3次以上の項も考慮して、より正確なガンマ関数の近似式(漸近展開)を求めていく。考え方はそれほど難しくないのだが、やや煩わしい計算が多いので結果だけを知りたい人は適当に読み流してくれてよい。
まず準備として次の形の積分を計算できるようにする: \begin{equation} I_{k} = \int_{-\infty}^{\infty} x^{k} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx \5 ( \alpha \gt 0 ) \end{equation} ただし \(k=0,1,2,\dots\) である。まず \(k\) が奇数の場合を考えると、被積分関数は奇関数になるから積分区間の対称性によってこの積分は直ちに \(0\) になることがわかる。次に \(k=0\) の場合を考えると、これはガウス積分の公式\eqref{gauss}を使って \begin{equation} I_{0} = \int_{-\infty}^{\infty} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx = \sqrt{\frac{2\pi}{\alpha}} \label{gauss2} \end{equation} となる。さて、\(k\) が \(2\) 以上の偶数となる場合だが、この場合は部分積分を行うことで \begin{align*} I_{k} &= \int_{-\infty}^{\infty} x^{k} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx \\[8pt] &= -\frac{1}{\alpha} \int_{-\infty}^{\infty} x^{k-1} \, \frac{d}{dx} \biggl( \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \biggr) \, dx \\[8pt] &= -\frac{1}{\alpha} \biggl[ x^{k-1} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \biggr]_{-\infty}^{\infty} + \frac{k-1}{\alpha} \int_{-\infty}^{\infty} x^{k-2} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx \\[8pt] &= \frac{k-1}{\alpha} \, I_{k-2} \end{align*} という漸化式が得られるので、上で求めた \(I_{0}\) を初期値とすることで \begin{align} &I_{2} = \int_{-\infty}^{\infty} x^{2} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx = \sqrt{\frac{2\pi}{\alpha}} \frac{1}{\alpha} \\[8pt] &I_{4} = \int_{-\infty}^{\infty} x^{4} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx = \sqrt{\frac{2\pi}{\alpha}} \frac{3}{\alpha^{2}} \\[8pt] &I_{6} = \int_{-\infty}^{\infty} x^{6} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx = \sqrt{\frac{2\pi}{\alpha}} \, \biggl( \frac{3\cdot5}{\alpha^{3}} \biggr) \\[8pt] &I_{8} = \int_{-\infty}^{\infty} x^{8} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx = \sqrt{\frac{2\pi}{\alpha}} \, \biggl( \frac{3\cdot5\cdot7}{\alpha^{4}} \biggr) \\[8pt] &I_{10} = \int_{-\infty}^{\infty} x^{10} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx = \sqrt{\frac{2\pi}{\alpha}} \, \biggl( \frac{3\cdot5\cdot7\cdot9}{\alpha^{5}} \biggr) \\[8pt] &I_{12} = \int_{-\infty}^{\infty} x^{12} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx = \sqrt{\frac{2\pi}{\alpha}} \, \biggl( \frac{3\cdot5\cdot7\cdot9\cdot11}{\alpha^{6}} \biggr) \label{gauss3} \end{align} などが順次求まる。
それではガンマ関数のより正確な近似式を計算していこう。ガンマ関数の積分表示\eqref{gamma3}を再掲しておく: \begin{equation*} \varGamma(\alpha) = \int_{-\infty}^{\infty} \exp f(x) \, dx \end{equation*} ただし \begin{equation*} f(x) = ( \alpha \ln \alpha - \alpha ) - \frac{\alpha}{2!} ( x - \ln \alpha )^{2} - \frac{\alpha}{3!} ( x - \ln \alpha )^{3} - \frac{\alpha}{4!} ( x - \ln \alpha )^{4} - \dotsb \end{equation*} である。これに積分変数の変換 \(x\to x+\ln\alpha\) を行うと \begin{equation} \varGamma(\alpha) = \int_{-\infty}^{\infty} \exp f(x+\ln\alpha) \, dx \label{gamma4} \end{equation} \begin{equation} f(x+\ln\alpha) = ( \alpha \ln \alpha - \alpha ) - \frac{\alpha}{2!} x^{2} - \frac{\alpha}{3!} x^{3} - \frac{\alpha}{4!} x^{4} - \dotsb \end{equation} となり、式\eqref{gamma4}の被積分関数のあらわな表式は \begin{equation} \exp f(x+\ln\alpha) = \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \: \prod_{k=3}^{\infty} \exp \Bigl( -\frac{\alpha}{k!} x^{k} \Bigr) \label{kernel} \end{equation} となる。前々節の計算では、この式の右辺の無限乗積の部分を \(1\) と近似したのであるが、ここでは近似の精度を一歩上げるため、無限乗積の中の指数関数をテイラー展開し、\(x\) のべきの小さい項も考慮することにする。\(x^{12}\) 以下の項を拾うことにして \begin{align} \prod_{k=3}^{\infty} \exp \Bigl( -\frac{\alpha}{k!} x^{k} \Bigr) &\simeq \Bigl( 1 - \frac{\alpha}{3!} x^{3} + \frac{\alpha^{2}}{2\cdot3!^{2}} x^{6} - \frac{\alpha^{3}}{6\cdot3!^{3}} x^{9} + \frac{\alpha^{4}}{24\cdot3!^{4}} x^{12} \Bigr) \notag \\ &\times \Bigl( 1 - \frac{\alpha}{4!} x^{4} + \frac{\alpha^{2}}{2\cdot4!^{2}} x^{8} - \frac{\alpha^{3}}{6\cdot4!^{3}} x^{12} \Bigr) \notag \\[3pt] &\times \Bigl( 1 - \frac{\alpha}{5!} x^{5} + \frac{\alpha^{2}}{2\cdot5!^{2}} x^{10} \Bigr) \times \Bigl( 1 - \frac{\alpha}{6!} x^{6} + \frac{\alpha^{2}}{2\cdot6!^{2}} x^{12} \Bigr) \label{prod} \\[3pt] &\times \Bigl( 1 - \frac{\alpha}{7!} x^{7} \Bigr) \times \Bigl( 1 - \frac{\alpha}{8!} x^{8} \Bigr) \times \Bigl( 1 - \frac{\alpha}{9!} x^{9} \Bigr) \times \Bigl( 1 - \frac{\alpha}{10!} x^{10} \Bigr) \notag \\[3pt] &\times \Bigl( 1 - \frac{\alpha}{11!} x^{11} \Bigr) \times \Bigl( 1 - \frac{\alpha}{12!} x^{12} \Bigr) \notag \end{align} と近似しよう。さて、この積を展開すると \begin{equation*} \prod_{k=3}^{\infty} \exp \Bigl( -\frac{\alpha}{k!} x^{k} \Bigr) \simeq 1 + \sum_{k=3}^{12} a_{k} x^{k} + ( x \ \text{の13乗以上の項} ) \end{equation*} という形になるのだが、今は \(x^{12}\) までを残す近似としたいので、\(x^{13}\) 以上の項は無視する。無視せずに残った部分を式\eqref{gamma4}や\eqref{kernel}に代入すると \begin{equation*} \varGamma(\alpha) \sim \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \int_{-\infty}^{\infty} \Bigl( 1 + \sum_{k=3}^{12} a_{k} x^{k} \Bigr) \, \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx \end{equation*} となり、先ほど求めたガウス積分の一連の公式を使えるようになる。すなわち \(x\) の奇数次の項は \(0\) となるため考えなくてよいし、\(x\) の偶数次の項には公式\eqref{gauss2}-\eqref{gauss3}を使う。そこで \(x^{12}\) 以下の偶数次の項だけを拾い出しながら式\eqref{prod}を展開していこう(それ以外の関係ない項は書き落とす): \begin{align*} \prod_{k=3}^{\infty} \exp \Bigl( -\frac{\alpha}{k!} x^{k} \Bigr) \simeq 1 &+ \biggl( - \frac{\alpha}{4!} \biggr) \, x^{4} + \biggl( \frac{\alpha^{2}}{2\cdot3!^{2}} - \frac{\alpha}{6!} \biggr) \, x^{6} + \biggl( \frac{\alpha^{2}}{3!\cdot5!} + \frac{\alpha^{2}}{2\cdot4!^{2}} - \frac{\alpha}{8!} \biggr) \, x^{8} \\[3pt] &+ \biggl( -\frac{\alpha^{3}}{2\cdot3!^{2}\cdot4!} + \frac{\alpha^{2}}{3!\cdot7!} + \frac{\alpha^{2}}{4!\cdot6!} + \frac{\alpha^{2}}{2\cdot5!^{2}} - \frac{\alpha}{10!} \biggr) \, x^{10} \\[3pt] &+ \biggl( \frac{\alpha^{4}}{24\cdot3!^{4}} - \frac{\alpha^{3}}{3!\cdot4!\cdot5!} - \frac{\alpha^{3}}{2\cdot3!^{2}\cdot6!} - \frac{\alpha^{3}}{6\cdot4!^{3}} \\[3pt] &\4 + \frac{\alpha^{2}}{3!\cdot9!} + \frac{\alpha^{2}}{4!\cdot8!} + \frac{\alpha^{2}}{5!\cdot7!} + \frac{\alpha^{2}}{2\cdot6!^{2}} - \frac{\alpha}{12!}\biggr) \, x^{12} \end{align*} あとは積分公式を使って \begin{equation} \varGamma(\alpha) \sim \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \int_{-\infty}^{\infty} \Bigl( 1 + a_{4} x^{4} + a_{6} x^{6} + a_{8} x^{8} + a_{10} x^{10} + a_{12} x^{12} \Bigr) \, \exp \Bigl( -\frac{\alpha}{2} x^{2} \Bigr) \, dx \label{asympt2} \end{equation} を計算すればよい。積分公式\eqref{gauss2}-\eqref{gauss3}と式\eqref{asympt2}をながめていると結果が次の形になることを予想できるだろうか: \begin{equation} \varGamma(\alpha) \sim \sqrt{\frac{2\pi}{\alpha}} \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \Bigl( 1 + \frac{c_{1}}{\alpha} + \frac{c_{2}}{\alpha^{2}} + \frac{c_{3}}{\alpha^{3}} + \frac{c_{4}}{\alpha^{4}} + \frac{c_{5}}{\alpha^{5}} \Bigr) \label{asympt3} \end{equation} ここでは最初の2つの係数 \(c_{1},c_{2}\) だけを求めることとする(実は \(c_{3}\) 以降を正確に求めるためには \(x^{14}\) 以上の項もきちんと考慮しなければならない)。まず \(c_{1}\) は \(x^{4},x^{6}\) に比例する項の積分から出てくる: \begin{equation*} c_{1} = -\frac{3}{4!} + \frac{3\cdot5}{2\cdot3!^{2}} = \frac{1}{12} \end{equation*} \(c_{2}\) のほうは \(x^{6},x^{8},x^{10},x^{12}\) に比例する項の積分から出てきて \begin{equation*} c_{2} = -\frac{3\cdot5}{6!} + \frac{3\cdot5\cdot7}{3!\cdot5!} + \frac{3\cdot5\cdot7}{2\cdot4!^{2}} - \frac{3\cdot5\cdot7\cdot9}{2\cdot3!^{2}\cdot4!} + \frac{3\cdot5\cdot7\cdot9\cdot11}{24\cdot3!^{4}} = \frac{1}{288} \end{equation*} となる。これらを式\eqref{asympt3}に代入し \(c_{3},c_{4},c_{5}\) を無視するとガンマ関数の漸近展開 \begin{equation*} \varGamma(\alpha) \sim \sqrt{\frac{2\pi}{\alpha}} \Bigl( \frac{\alpha}{e} \Bigr)^{\alpha} \Bigl( 1 + \frac{1}{12\alpha} + \frac{1}{288\alpha^{2}} \Bigr) \end{equation*} が得られる。\(\alpha\) を \(x\) と置けば \begin{equation} \varGamma(x) \sim \sqrt{\frac{2\pi}{x}} \Bigl( \frac{x}{e} \Bigr)^{x} \Bigl( 1 + \frac{1}{12x} + \frac{1}{288x^{2}} \Bigr) \5 ( x \gg 1 ) \label{asympt4} \end{equation} である。
この式で \(x=n+1\) と置いて \(n!\) の近似値を計算すると次の表のようになる。近似の精度が式\eqref{stirling2}と比べて著しくよくなっていることがわかるだろう。近似式\eqref{asympt4}はいつも真値より少し大きい値を返しているから、漸近展開の次の補正項 \(c_{3}\) の符号は負になりそうである。
| \(n\) | \(n!\) | 近似式\eqref{asympt4} | 近似式\eqref{stirling2} |
|---|---|---|---|
| \(1\) | \(1\) | \(1.0003143\) | \(0.9595022\) |
| \(2\) | \(2\) | \(2.0001927\) | \(1.9454032\) |
| \(3\) | \(6\) | \(6.0002471\) | \(5.8765438\) |
| \(4\) | \(24\) | \(24.000509\) | \(23.603834\) |
| \(5\) | \(120\) | \(120.00148\) | \(118.34636\) |
| \(10\) | \(3628800\) | \(3628807.3\) | \(3601420.5\) |