「無限大」という名前の記号 \(\infty\) は高校数学にも現れる。例えば \begin{equation*} \lim_{x\to+\infty} f(x) = + \infty \end{equation*} のように。ただし、この式の意味は「\(\,x\) を限りなく大きくしていったとき \(f(x)\) がとる値も限りなく大きくなっていく(正の無限大に発散する)」というものであり、「\(\,x\) に \(+\infty\) を代入すると \(f(x)\) は \(+\infty\) という値をとる」という意味ではない。高校数学の範囲では、実数全体の集合 \(\mathbb{R}\) に \(+\infty\) や \(-\infty\) という新たな要素が追加されたわけではなかったのである。しかしながら、\(\infty\) という「数」をある程度きちんと導入することもできて、とくに複素数全体の集合 \(\mathbb{C}\) に \(\infty\) という1点を付け加えた集合では微分のような演算もきちんと定義される。このページでは複素数の1つとしての \(\infty\) の取り扱い方について簡単に説明していきたい。
拡張された複素平面
複素 \(z\) 平面から複素 \(w\) 平面への写像 \(w=1/z\) を考えよう。この写像によって \(z\) 平面上の原点を除いたすべての点は \(w\) 平面上の原点を除く点へ1対1でうつされる。
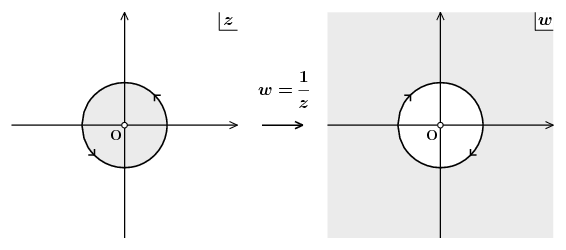
極座標を使って \begin{equation*} z = r e^{i\theta}, \4 w = \frac{1}{z} = \frac{1}{r} e^{-i\theta} \end{equation*} と表してみるとわかりやすいが、\(z\) 平面上の単位円の内側にある点(原点を除く)は \(w\) 平面の単位円の外側に、\(z\) 平面上の単位円の外側にある点は \(w\) 平面の単位円の内側にうつることになる。また単位円は単位円にうつるが、円周上の各点はもとの点とくらべて実軸に関して対称なところへ移動することになる(単位円を時計回りに1周するような経路は反時計回りに1周するような経路となる)。このように \(w=1/z\) という写像は、単位円の内側と外側を入れ替える写像としてはとても対称性のよい格好になっているが、\(z\) 平面においても \(w\) 平面においても、1点だけ原点を特別扱いしている。\(z\) 平面においては原点 \(\text{O}\) が除外点となっているし、\(w\) 平面においては原点にだけ像が存在しない(すなわち \(w\) 平面の原点へうつってくるような点が \(z\) 平面上に存在していない)。しかし、このような対称性のよい写像において、原点だけを特別扱いしてしまうのは少しもったいない気がする。多少無理をしてでも全複素平面で定義されるような写像としたいところである。それには \(w=1/z\) という写像によって、\(z\) 平面の原点がうつっていくような \(w\) 平面上の点と、\(w\) 平面の原点へうつってくるような \(z\) 平面上の点が存在すればよいのだが、もしそのような点があるとするならば、それは誰もが思いつくように原点から無限に遠く離れた点、無限遠点 \(\infty\) であろう。そこで複素数全体の集合 \(\mathbb{C}\) に1点 \({\infty}\) を加えた新しい集合 \(\overline{\mathbb{C}}=\mathbb{C}\cup\{\infty\}\) を考える。これを「拡張された複素平面」という。\(\overline{\mathbb{C}}=\mathbb{C}\cup\{\infty\}\) を考えるとはどういうことかというと、例えば \begin{equation*} f(\infty) = \infty \end{equation*} のような書き方が許されるということである。すなわち \(\infty\) が1つの数として扱われるようになる。今後は \(\infty\) も複素数の1つとして扱うが、以下で見るように実際上 \(\infty\) はいつも特別扱いされることになる。
ところで上では \(\infty\) を「1点」と書いたが、\(\infty\) と言っても \(+\infty\) や \(-\infty\)、あるいは \(\infty\cdot e^{i\theta}\) のようにいろいろな偏角をもつものがあると考えた人がいるかもしれない。しかし、複素関数論ではこれらの点をすべて同一視して区別はしない。\(+\infty\) も \(-\infty\) もすべて同じ1つの点 \(\infty\) として扱うのである。(ただし、実解析(例えばルベーグ積分)では \(\mathbb{R}\) に \(+\infty\) と \(-\infty\) の2点を加えた拡張された実数 \(\overline{\mathbb{R}}=\mathbb{R}\cup\{-\infty,+\infty\}\) というものを考えることがある。) 無限遠点に対しては原点と同じように偏角は考えない。これは無限遠点が \(w=1/z\) によって原点と対応していることを思い起こせばもっともなことだろう。イメージ的には、無限に広がった複素平面のふろしきを四方八方から包み込み、1つの無限遠点で結んでしまうような感じだ。このように考えると拡張された複素平面 \(\overline{\mathbb{C}}\) は平面というよりも球面の形に似ており、そのため拡張された複素平面のことを「リーマン球面」と呼ぶこともある。球面というのは無限に広がった平面にくらべコンパクトな印象である。
演算規則
拡張された複素平面上において、\(\infty\) を含む四則演算は次のように定義される。\(z\neq0,\infty\) とするとき、まず加法については \begin{equation} z + \infty = \infty + z = \infty, \5 0 + \infty = \infty + 0 = \infty, \5 \infty + \infty: \text{定義しない} \label{addition} \end{equation} と定める。せっかく \(\infty\) という数を追加したのに \(\infty+\infty\) が定義されないことを不満に思う人がいるかもしれない。しかし、\(\infty\) を含まない通常の複素数の世界でも \(z/0\) が定義されなかったように、ほかの計算との整合性をとるためには、これを定義しないでおいたほうが便利なのである。次に乗法について \begin{equation} z \cdot \infty = \infty \cdot z = \infty, \5 0 \cdot \infty, \ \ \infty \cdot 0: \text{定義しない}, \5 \infty \cdot \infty = \infty \label{multiplication} \end{equation} と定義する。とくに重要なのは除法の性質である。拡張された複素平面においては \(w=1/z\) という写像によって \(0\) と \(\infty\) が対応することより \begin{equation*} \frac{1}{0} = \infty, \4 \frac{1}{\infty} = 0 \end{equation*} が成り立つべきであるが、これらと乗法の性質\eqref{multiplication}に整合性をもたせるために、除法の演算規則は \begin{equation} \frac{z}{0} = \frac{\infty}{0} = \infty, \5 \frac{z}{\infty} = \frac{0}{\infty} = 0, \5 \frac{0}{0}, \ \ \frac{\infty}{\infty}: \text{定義しない} \end{equation} とするのがよい。なお、\(\infty\) を含む引き算については \(-\infty=(-1)\cdot\infty=\infty\) と解釈することで、加法の規則\eqref{addition}と同じ形になるが、とくに \(\infty-\infty\) が定義されないことに注意しよう(\(\,\infty-\infty=0\) ではない)。
以上で無限遠点を含む四則演算を行うことができるようになったわけだが、実際に無限遠点における関数の値を評価するときなどには、この規則をそのまま使うだけではうまくいかないことがある。例えば、関数 \begin{equation*} f(z) = \frac{z}{z+1} \end{equation*} の \(z=\infty\) における値を計算すると \begin{equation*} f(\infty) = \frac{\infty}{\infty+1} = \frac{\infty}{\infty} \end{equation*} となるため、一見すると \(f(\infty)\) は定義されないように見える。しかし、\(z=1/w\) と置いて \begin{equation*} f(z) = f(1/w) = \frac{(1/w)}{(1/w)+1} = \frac{1}{1+w} =: g(w) \end{equation*} と変形し、\(z=\infty\) が \(w=0\) に対応していたことを思い出すと、\(f(\infty)\) を評価するということは \(g(0)\) を計算するのと同じであることに気づく。したがって \begin{equation*} f(\infty) = g(0) = \frac{1}{1+0} = 1 \end{equation*} となり、先ほどは計算不能になったにもかかわらず、今度は正しい結果 \(f(\infty)=1\) が得られる。この例からもわかるように、無限遠点における関数の値を直接評価するよりも、変換 \(z=1/w\) によって対応する \(w\) 平面の原点で関数値を評価したほうが計算不能におちいることが少ない(もちろん、状況によっては \(z\) に \(\infty\) を直接代入したほうがよいこともある)。基本的に、無限遠点において関数値を評価したい場合は、まず変換 \(z=1/w\) を行って、\(w=0\) での値を計算するように習慣づけるとよい。\(\infty\) よりも \(0\) に対してのほうが定義されない演算が少ないからである。
無限遠点における微分
関数 \(f(z)\) の無限遠点における微分可能性は、\(z=1/w\) によって \(w\) 平面にうつした関数の原点における微分可能性によって定義される。すなわち \begin{equation*} f(z) = f(1/w) = g(w) \end{equation*} と置いたとき、もし \(g'(0)\) が存在するならば \(f(z)\) は無限遠点において微分可能とする。ここで注意したいのは、拡張された複素平面においては、微分係数が \(\infty\) という値をとってもよいのだが、その場合には相変わらず微分可能とは言わない(微分係数は存在しない)ことである。ところで \begin{equation*} g'(w) = \frac{d}{dw} f(1/w) = -\frac{1}{w^{2}} f'(1/w) \end{equation*} より \(f'(z)=-w^{2}\1g'(w)\) が成り立つから、もし \(g'(0)\) が存在する(有限である)ならば \begin{equation} f'(\infty) = \Bigl[ -w^{2} g'(w) \Bigr]_{w=0} = 0 \end{equation} でなければならない。そのため、もし \(f(z)\) が無限遠点で微分可能であるならば、無限遠点における微分係数 \(f'(\infty)\) は必ず \(0\) となる。なお、もし \(g(w)\) が原点で微分可能なだけでなく、原点を含む適当な領域(これはどんなに小さくてもよい)のすべての点で微分可能ならば、\(f(z)\) は無限遠点において「正則」であるという。
無限遠点におけるローラン展開
関数 \(f(z)\) の無限遠点 \(z=\infty\) におけるローラン展開は、変換 \(z=1/w\) によって、\(g(w)=f(1/w)\) の原点まわりのローラン展開として定義される。\(f(z)\) が原点を中心とする円環領域 \(0\le R\lt|z|\lt\infty\) で一価正則であるとき(ローラン展開なので無限遠点は正則点でなくてもよい)、\(g(w)\) は \(0\lt|w|\lt1/R\) で一価正則となるから、この領域で \(w=0\) のまわりのローラン展開 \begin{equation*} g(w) = \sum_{n=-\infty}^{\infty} a_{n} w^{n}, \4 a_{n} = \frac{1}{2\pi i} \oint_{C_{0}} \frac{g(w)}{w^{n+1}} dw \end{equation*} が成り立つ。ただし、積分路 \(C_{0}\) は \(0\lt|w|\lt1/R\) の領域に置かれた原点を囲むような単純閉曲線で、積分路の向きは原点を左手に見ながら進む方向(反時計回り)である。(単純閉曲線とは自身と交わらない閉じた曲線のこと。なお、このページでは「曲線」といえば有限の長さをもつものだけを考えるものとする。) \(w\) をもとの変数 \(z\) に戻すと \begin{equation} f(z) = \sum_{n=-\infty}^{\infty} \frac{a_{n}}{z^{n}} = \sum_{n=1}^{\infty} a_{-n} \1 z^{n} + \sum_{n=0}^{\infty} \frac{a_{n}}{z^{n}} \label{laurent} \end{equation} となる。展開係数のほうは \(dw/dz=-1/z^{2}\) より \begin{align} a_{n} &= \frac{1}{2\pi i} \oint_{C_{\infty}} \frac{f(z)}{(1/z)^{n+1}} \frac{dw}{dz} dz \notag \\[3pt] &= -\frac{1}{2\pi i} \oint_{C_{\infty}} \frac{f(z)}{z^{-n+1}} dz \label{an} \end{align} になる。ただし、積分路 \(C_{\infty}\) は \(R\lt|z|\lt\infty\) にある原点を囲むような単純閉曲線で、積分路の向きは無限遠点を左手に見ながら進む方向(時計回り)である。式\eqref{laurent}右辺の最初の級数 \(\sum\limits_{n=1}^{\infty}a_{-n}z^{n}\) を主要部、または特異部という。この主要部が \(k\) 次の多項式となる場合、\(z=\infty\) を \(k\) 位の極であるといい、主要部が無限級数となる場合には \(z=\infty\) を真性特異点という。また主要部が存在しない場合、\(f(z)\) は \(z=\infty\) において正則であるという。
無限遠点を考えない場合、関数 \(f(z)\) の点 \(\alpha\) における留数 \(\Res(\alpha)\) は \begin{equation*} \Res(\alpha) = \frac{1}{2\pi i} \oint_{C_{\alpha}} f(z) \, dz \end{equation*} と定義されるが(\(\,C_{\alpha}\) は点 \(\alpha\) を囲む単純閉曲線で、その内部から点 \(\alpha\) を除いた領域で \(f(z)\) が正則となるように選ぶ)、無限遠点における留数 \(\Res(\infty)\) も相変わらず次のように定義される: \begin{equation} \Res(\infty) = \frac{1}{2\pi i} \oint_{C_{\infty}} f(z) \, dz \label{res} \end{equation} ただし、積分路 \(C_{\infty}\) は無限遠点を左手に見ながら進むような経路(時計回り)で、その外部(無限遠点側)から無限遠点を除いた領域で \(f(z)\) は正則である。式\eqref{res}を式\eqref{an}と比較してみると \begin{equation} \Res(\infty) = -a_{1} \end{equation} であることがわかる。無限遠点以外の正則点の留数はいつも \(0\) であったが、無限遠点の留数 \(\Res(\infty)\) は、\(f(z)\) が \(\infty\) において正則であったとしても \(0\) になるとは限らないので注意しよう(\(\,a_{1}\) は主要部の展開係数ではないため)。
最後に留数定理の拡張について述べる。
以上、無限遠点と拡張された複素平面における計算方法について簡単に見てきたが、この拡張された複素数というのは代数学で言うところの「体」を構成してはいない(体とは、実数や複素数、有理数のような四則演算を自由に行うことができる数のこと)。それは無限遠点を含む四則計算において結果の定義されない演算が多くあらわれたことからも理解できると思う。しかしながら数学の超準解析という分野においては、通常の実数の体系と矛盾することなく無限大や無限小という量が取り入れられており、その全体の超実数と呼ばれる数体系は体を構成するという。また微分や積分のような演算も、極限のような曖昧な操作や \(\varepsilon\)-\(\delta\) 論法のような複雑で直観的でない考察を行うことなく、厳密に定義されるという。